Fonctionnement

Les algorithmes génétiques sont une méthode de recherche de solution de problèmes complexes inspirée du modèle de l’évolution étudié en biologie. Ils ont l’avantage de permettre de trouver des solutions à un problème spécifique (par exemple le “Problème du voyageur de commerce”), particulièrement s’il implique de rechercher parmi un grand nombre de solutions possibles, sans obliger le programmeur à avoir une compréhension analytique de la situation.

Les algorithmes génétiques imitent la manière dont les organismes se reproduisent et évoluent dans la nature. Il est bien sûr possible de faire fonctionner des algorithmes génétiques sans la multiplicité de variables qui existent dans le monde réel. Un algorithme génétique doit seulement mettre au point des règles pour :

• la compétition
• la survie
• la reproduction

Le processus implique 4 étapes principales :

1. initialisation : une population de départ, composée de plusieurs chromosomes, est créée de manière aléatoire. Chaque élément d’information composant un chromosome est appelé un allèle.
2. valeur sélective : chaque chromosome d’une population donnée possède une valeur sélective (fitness score) dont on choisira les critères de calcul.
3. reproduction : les chromosomes sont choisis pour être parents de la génération suivante. Les chromosomes les plus résistants (en fonction de leur valeur sélective) ont plus de chance d’être choisis que les autres. La reproduction est accomplie par clonage ou en mélangeant les informations de deux chromosomes. Par ailleurs, des mutations peuvent advenir (généralement, avec une faible probabilité), suivant un nombre aléatoire ou un outil de distribution statistique tel que la fonction de Gauss, en introduisant une variation aléatoire d’une des allèles.
4. nouvelle génération : on peut reprendre le processus au stade 2

Deux allèles ou plus forment un chromosome. L’ordre des allèles est généralement signifiant.

Les chromosomes, représentant des individus, sont regroupés en populations.

A chaque chromosome correspond une valeur sélective, calculée par comparaison avec les autres, par une fonction mathématique, ou par des règles.

La technique la plus connue pour la reproduction est l’hybridation, qui définit un point de mélange entre les deux chromosomes (appelé point d’hybridation, ici représenté par le signe |) :

Chromosome père	Chromosome mère	Descendant
abd | bcbag	bdd | cbabc	abd | cbabc

Exemple avec plusieurs points de crossover (d’hybridation) :

Chromosome père	Chromosome mère	Descendant
ab | db | cb | ag	bd | dc | ba |bc	ab | dc | cb | bc

Les chromosomes s’accouplent sous conditions, avec ceux qui sont les plus résistants.

• 2 chromosomes peuvent produire un ou plusieurs descendants (qui les remplacent)
• chaque chromosome est créé soit en clonant un parent, soit en mélangeant leurs allèles avec deux points de transitions ou plus
• chaque chromosome fils peut subir des mutations de l’allèle (une seule ou plusieurs)

Le but d’une population est d’aller vers le chromosome le plus résistant.

La valeur sélective (fitness score) est donc la clé. Elle exprime quelles sont les priorités du système. Celle-ci peut être :

• un jugement intuitif de l’artiste
• un jugement intuitif du public
• une évaluation basée sur des critères comme l’échelle, les ratios, etc.
• un ensemble de règles

Lorsque plusieurs solutions (générations) optimales sont trouvées, le processus s’arrête.

Les chromosomes peuvent être, du plus simple au plus complexe :

• une chaîne de bits (soit en code binaire, soit fréquemment en “code de Gray”, permettant en moyenne moins de grands changements et plus de petits changements), puis les gènes sont définis par une table de correspondance.
• une structure de données avec un nombre de paramètres spécifiques au phénotype
• un format variable, par exemple : programmes pouvant être compilés et assemblés, programmes pouvant être interprétés par une machine virtuelle, formules mathématiques, instructions pour construction modulaire…

Il convient de noter que phénotype (expression des données) et génotype (données codées) se confondent fréquemment dans les modèles d’algorithmes génétiques. Dans la réalité “biologique” des choses, il peut arriver que les chromosomes (génotypes) ne soient pas entièrement exprimées de manière physique (phénotype). Dans de tels cas, l’allèle dit récessif, même non exprimé, peut néanmoins être transmis à la génération suivante. Ce processus peut amener plus de complexité et de richesse dans un algorithme génétique.

En musique

Les algorithmes génétiques sont un outil puissant pour générer des variations. Ils se prêtent bien à la génération d’un grand nombre de données (ce n’est pas pour rien que cette technique est notamment utilisée, dans les arts graphiques, pour créer des personnages dans une foule, ou des arbres dans une forêt). On peut aussi l’utiliser dans le cadre de créations ou installations interactives, en faisant intervenir le spectateur pour sélectionner certains sons ou certaines images (en guise de valeur sélective).

L’intérêt musical des algorithmes génétiques se manifeste surtout avec un grand nombre d’allèles (d’événements musicaux (phrases) ou caractéristiques sonores) et d’individus. Cela permet d’explorer une combinatoire avec un certain nombre de règles (modifiables éventuellement au fur et à mesure si le processus ne produit pas de résultats satisfaisants) en favorisant certaines combinaisons privilégiées a priori.

A ce titre, certains musicologues le comparent au processus normal d’un compositeur en recherche d’un développement pour son matériau, qu’il procède par l’improvisation ou par la recherche sur le papier : “In fact, mutation is closely related to notions of development, which lie at the heart of western musical concepts of form and structure. It may even be possible to see development as directed mutation.”

Certains chercheurs ont également utilisé ce mécanisme pour sa propriété de résolution de problèmes, notamment pour trouver les paramètres FM qui permettent l’imitation d’un son instrumental.

Expérience : un instrument virtuel avec les algorithmes génétiques

Dans le but de présenter un exemple concret, imaginons que nous souhaitons construire un instrument virtuel associé à un contrôleur. Mettons que nous souhaitons associer un son différent à chaque pad (ou à chaque touche), mais que le son d’un même pad soit à chaque fois légèrement différent, selon la vélocité ou n’importe quel autre geste instrumental. Nous avons donc besoin de générer plusieurs sons ayant un même air de famille.

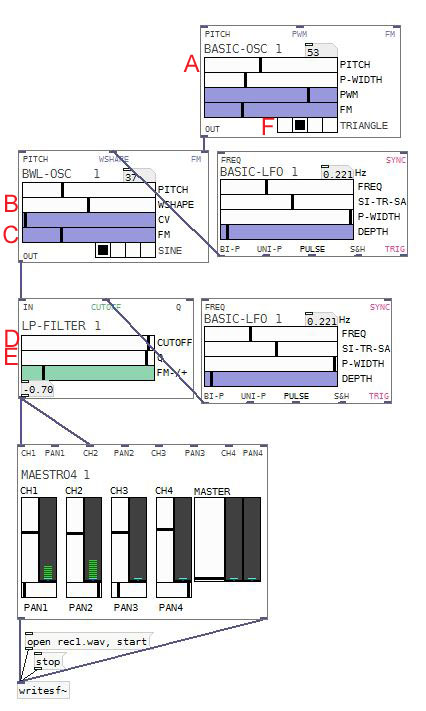
On part de l’idée qu’un son sera un chromosome. Chaque chromosome sera composé arbitrairement de 6 allèles (A B C D E F) correspondant à 6 paramètres d’un synthétiseur minimaliste construit dans AUTOMATONISM (PureData). Chacun est un nombre compris entre 0 et 127.

A – hauteur de la modulante (Module BWL-OSC – Pitch)
B – quantité d’harmoniques dans le son modulé (Module BWL-OSC – Wshape)
C – index de la modulation fm (Module BWL-OSC – FM)
D – fréquence du filtre passe-bas (Module LP – cutoff)
E – largeur du filtre passe-bas (Module LP – Q)
F – forme d’onde du son modulant (Module Basic-Osc – sine–triangle–saw-pulse)

La hauteur de la fondamentale sera systématiquement 37 en notation MIDI (69,3 Hz)

1. initialisation : population générée aléatoirement (10 individus par génération).
2. calcul de la valeur sélective : les valeurs étant se rapprochant de 10 % des valeurs du son de référence marquent un point.
3. accouplement : seuls les gènes qui ont marqué le score sont échangés entre les parents et présents dans le chromosome fils. Si le gène qui a marqué le score est le même chez les deux parents, on choisit le plus proche de l’original. Tous les autres gènes sont retirés au sort.

Les 6 paramètres du son de référence :

101 81 32 37 105 37

Processus :

1. chaque individu de la génération 0 (aléatoire) est évalué en fonction de sa valeur sélective
2. un système de probabilités permet de définir 10 couples en fonction de leur résistance : un individu qui a obtenu un score de 2 a deux fois plus de chance d’être choisi pour former un couple qu’un individu ayant obtenu un score de 1.
3. chaque couple ne produit qu’un seul descendant.
4. chaque descendant est évalué sur sa résistance et ainsi de suite

Bien évidemment, ce protocole vaut surtout pour la démonstration, le matériel de départ étant trop limité et les critères de sélection trop simplistes pour produire des variations musicalement dignes d’intérêt. Il permet néanmoins de mesurer pleinement l’efficacité du processus qui parvient à se stabiliser en 10 générations et à proposer une série de sons répondant aux critères formulés initialement :

Génération 0 :

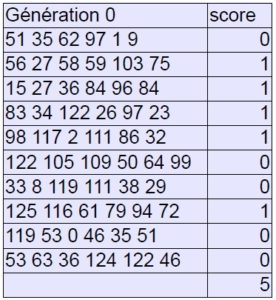
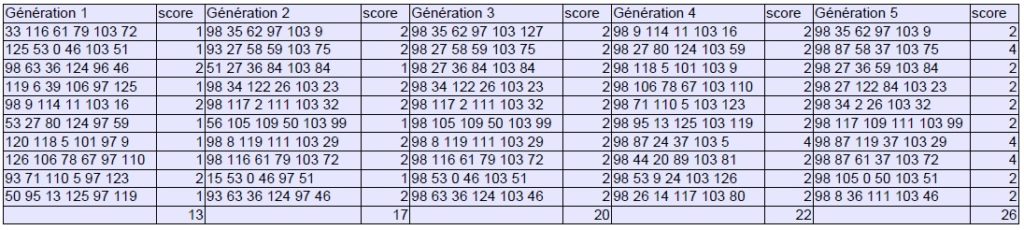
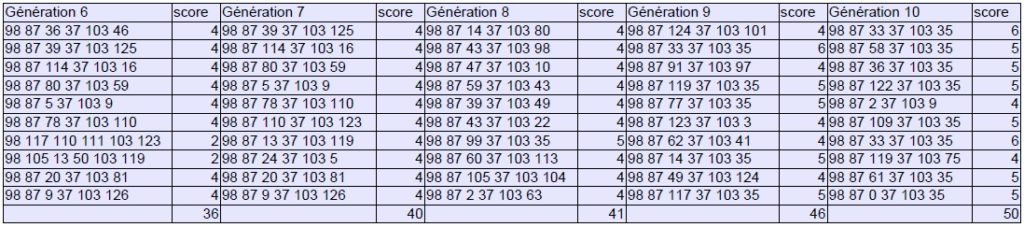
Générations 1 à 10 :

On pourrait imaginer, pour rendre l’expérience plus riche, augmenter le nombre de gènes (effets, enveloppes, spatialisation…) afin de multiplier les possibilités d’échange de matériel génétique entre parents. Il serait également intéressant d’introduire un facteur de mutation pouvant toucher aléatoirement une partie de la population selon une proportion donnée (20% par exemple) où les gènes gagnants seraient retirés en sort, mais cette fois-ci dans les 10 % acceptables, pour éviter à certains paramètres d’atteindre rapidement un effet de plateau.

Générer des rythmes (Christopher Ariza)

Le compositeur Christopher Ariza a créé une librairie dans AthenaCL (langage Python) appelée GArthm.py. Dans ce système, la valeur sélective est calculée en fonction de sa ressemblance avec un rythme cible. Il ne s’agit donc pas de résoudre un problème (la solution est connue d’emblée) mais de s’intéresser au parcours qui conduira vers la solution.

L’unité rythmique est exprimée sous la forme d’un code à trois chiffres placés entre parenthèses :

1. diviseur
2. multiplicateur
3. note ou silence (1 ou 0)

Par exemple :

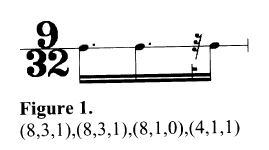
Le rythme est ensuite calculé en fonction d’une pulsation de référence : on divise cette dernière par le diviseur, puis on multiplie par le multiplicateur. Cette méthode permet également de décrire des rythmes impairs ou irrationnels :

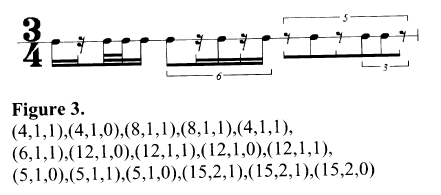
Cette manière de structurer l’information a également l’avantage de présenter un taux important de redondance. En effet, on peut noter un même rythme de plusieurs manières différentes (par exemple, (6,2,1) exprime la même durée que (3,1,1)). Cette redondance est souhaitée par le compositeur afin d’assurer des transitions aussi progressives que possibles entre les différentes variations d’un rythme.

La taille de la population est arbitrairement fixée à 20 individus (n = 20).

Les chromosomes de la population initiale ont tous la même longueur que le rythme cible (“fit-rhythm” ou “fit-chromosome”), et la même durée. Les allèles de chaque chromosome sont choisis aléatoirement parmi ceux présents dans le rythme-cible. C’est la génération 0 (i = 0).

Afin de produire la génération suivante (i = 1), des membres de la génération 0 sont choisis pour se reproduire entre eux.

Les chromosomes les plus ressemblants avec le rythme-cible ont plus que de chances que les autres d’être choisis comme individus reproducteurs, même si le processus reste statistique.

Ariza utilise une méthode souvent choisie dans ce cas de figure, le “roulette wheel sampling”, que l’on pourrait décrire sommairement comme une roulette de casino dont les divisions seraient proportionnelles à la valeur sélective (donc la bille aurait plus de chances de tomber sur l’une de ces divisions).

L’accouplement se déroule en deux étapes : l’hybridation et la mutation. Il y a un taux d’hybridation déterminé : 70% de la population. Cette dernière consiste en une hybridation à deux points, autour desquels les allèles des deux parents s’échangent. Les 30% restant clonent simplement leur chromosome. On s’inspire là encore du modèle naturel, où l’évolution s’exprime principalement par l’hybridation, et où la mutation n’est qu’une manière d’assurer à une population un minimum de variation à un point donné.

Le taux de mutation est également prédéfini (0,001, soit 0,1%), la probabilité d’une mutation étant indépendante de l’hybridation. La mutation peut être de 5 sortes :

1. équivalence du ratio (changement de la notation qui n’affecte pas le résultat sonore : par exemple, (3,1,0) devient (6,2,0)
2. mutation du diviseur : (3,1,0) devient (4,1,0)
3. mutation du multiplicateur : (3,1,0) devient (3,2,0)
4. transformation d’une note en silence, ou réciproquement : (3,1,0) devient (3,1,1)
5. rétrograde d’un segment du chromosome entre 2 points aléatoires

Ariza prévoit également dans son système un processus “d’élitisme” permettant à de rares chromosomes, les plus proches du rythme-cible, de subsister inchangés à la génération suivante, sans subir ni hybridation ni mutation. Cela permet d’augmenter la stabilité du modèle, notamment si le rythme-cible est particulièrement long ou complexe.

La mesure de ressemblance avec le rythme-cible prend en compte 5 critères, avec des pondérations spécifiques :

1. la durée totale des notes
2. la durée totale des silences
3. la durée totale du chromosome (sons + silences)
4. la durée des allèles divergents
5. la durée des valeurs divergentes

Créations musicales à base d’algorithmes génétiques

• Al Biles, improvisations de jazz avec le logiciel GenJam
• Peter Beyls, Drake Circus

Pistes de lecture

Cristyn Magnus, “Evolving electroacoustic music: the application of genetic algorithms to time-domain waveforms”, Proceedings of the 2004 International Computer Music Conference, 2004.

 

(Illustration : Ernst Haeckel, Kunstformen der Natur, Domaine public)