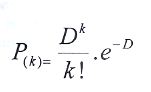Probabilités et stochastique

INDEX
1 – Probabilités et aléatoire
2 – Méthode de Monte-Carlo
3 – Fonction de Gauss
4 – Loi de Poisson

Probabilités et aléatoire

En mathématique, un processus stochastique (du grec “stochastês” : devin) permet de décrire des comportements en partie prévisible. Alors que ces formules sont utilisées en statistiques pour distinguer les motifs significatifs de simples phénomènes aléatoires (car dans la nature le hasard ressemble très rarement à du hasard), l’usage en musique est en quelque sorte inverse, en permettant l’organisation des données musicales.

Une probabilité est une fraction exprimant le rapport quantitatif entre deux ensembles d’événements : l’ensemble fondamental et un sous-ensemble de ce dernier, mesurant la proportion d’un événement spécifique incluse dans l’ensemble fondamental. Plus grande est la probabilité d’un événement, plus il est vraisemblable qu’il se produise effectivement. Comme la valeur calculée par la fonction est compris entre 0 et 1, on applique un mapping de normalisation (par exemple, en multipliant par le nombre de hauteurs). Si la probabilité d’un événement est de 0,11, il a 11% plus de chances d’arriver que les autres.

Les environnements de programmation (MaxMSP, Pure Data, Open Music) disposent tous d’un générateur de nombre pseudo-aléatoire. Attention, dans Pure Data, les nombres générés par l’objet [random] sont générés par une suite déterministe à répartition uniforme. En d’autres termes, le résultat généré sera à chaque fois le même en refermant un patch et en le ré-ouvrant. Afin de pallier ce problème, il faut utiliser l’objet [seed]. Cet objet doit envoyer un nombre différent à chaque utilisation de l’objet [random] et à l’ouverture du patch :

Exemple d’une suite de notes aléatoires générée avec un mapping de normalisation sur deux octaves chromatiques :

Méthode de Monte-Carlo

Très utilisée en physique, la méthode dite de Monte Carlo consiste à calculer une valeur par l’utilisation de procédés aléatoires. Un cas de vulgarisation connu est de déduire la surface d’une forme irrégulière au sein d’un carré : en criblant aléatoirement la surface du carré d’un très grand nombre de points, on compte le nombre de points tombés dans la forme et ceux tombés en-dehors.

Il y a un rapport d’équivalence :

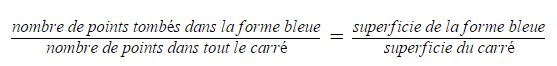
D’où :

En musique, on peut l’utiliser afin de définir une aire de probabilités pour certains événement sonores (les hauteurs et les durées) et exclure les valeurs qui ne correspondent pas à ces probabilités. Dans la Suite Illiac, Hiller et Isaacson s’en servent pour générer des suites aléatoires de nombres entiers dans un ambitus donné (dans cet exemple, entre 1 et 7) en partant d’un nombre décimal à 4 chiffres après la virgule :

Voyons un autre exemple :

  1. Tirer un nombre r au hasard entre 0 et 1
  2. Multiplier r par le nombre de hauteurs (* 12) et arrondir. Cela donne un résultat entre 0 et 11 qui correspond à l’un des éléments n de la table de probabilités
  3. Consulter la valeur de probabilité pour l’élément n (Pn). Tirer un nouveau nombre aléatoire r2. Si r2 est plus petit ou égal à Pn, accepter la valeur, sinon revenir à l’étape 1.

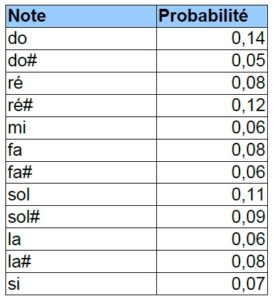
4. Même processus que 1 à 3 pour les durées.

Un exemple de tirage possible :

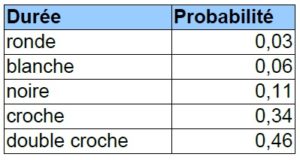
Une autre méthode aboutissant au même résultat consiste à additionner successivement les poids statistiques de chaque élément (note ou durée), afin de les considérer comme des seuils. Par exemple, en reprenant le tableau des durées, les seuils seront 0.03, 0.09 (0.03 + 0.06), 0.20 (0.09 + 0.11), etc. On produit ensuite une série de valeurs comprises entre 0 et 1. Chacune de ces valeurs étant comprise entre l’un des seuils ainsi définis, elle déclenche l’élément correspondant.

Télécharger le patch Pure data (distribution Purr data – anciennement Pd-extended)

L. Hiller et L. Isaacson, utilisent dans les Expériences 3 et 4 les pourcentages suivants, dans le cadre d’une musique tonale basée non pas sur l’analyse d’un corpus existant mais sur un calcul élémentaire mais astucieux prenant en compte le degré de consonance et la taille de chaque intervalle :

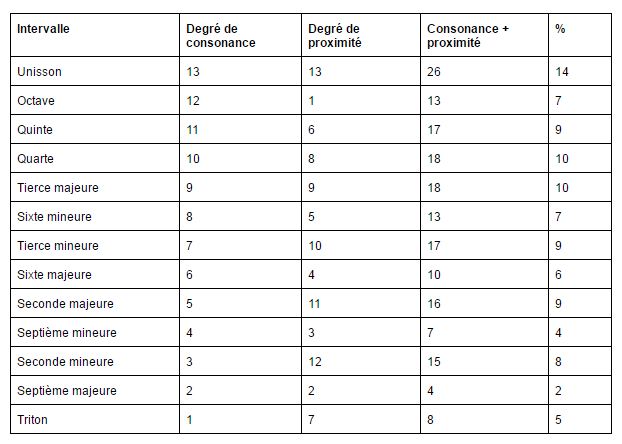
Il est intéressant de constater, comme le fait Laurent Fichet, que Pierre Barbaud propose des pourcentages assez similaires (si l’on prend en considération qu’il n’attribue pas de valeur à l’octave), avec une méthode différente basée sur les probabilités qu’un intervalle donné puisse produire une note qui se trouve elle aussi dans la même gamme diatonique (par exemple, seulement deux possibilités : mi-fa et si-do) :

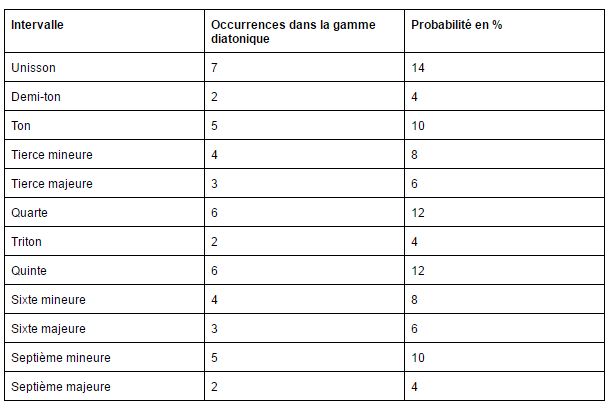
Fonction de Gauss

Les fonctions de probabilité permettent d’attribuer des valeurs de probabilité aux éléments de son ensemble. L’une des plus communément observées dans la nature est la distribution de Gauss (par exemple, la distribution des tailles dans une population donnée).

La fonction de Gauss montre une courbe caractéristique en forme de cloche :

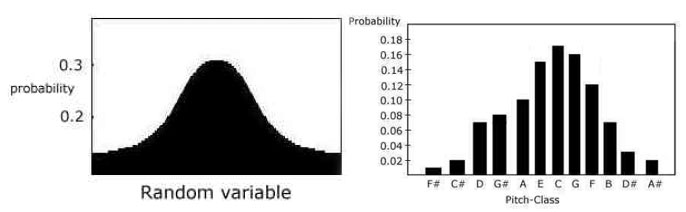
Elle est notamment utilisée par Xenakis pour définir les glissandis dans Pithoprakta.

Loi de Poisson

La loi de Poisson se retrouve dans de nombreux phénomènes, particulièrement les événements rares (crashs informatiques, catastrophes ferroviaires, …). En musique, la loi de Poisson est volontiers utilisée pour définir des densités d’un type d’événement donné.

“Pour tenter une explication de cette formule, imaginons une urne contenant 12 boules de couleurs différentes, dont une rouge. Si, dans une unité de temps quelconque, on procède à 2 extractions d’une boule de cette urne, en la replaçant à chaque fois après avoir noté la couleur sortie, théoriquement, chaque couleur a 1 chance de sortir 1 fois pendant cette unité de temps. En réalité, il faut un certain nombre de tirages (chacun de 12 boules) pour que, en moyenne, chaque couleur soit sortie une fois par tirage, car, au premier tirage, la rouge peut très bien sortir deux, trois ou quatre fois, et ne pas sortir du tout au deuxième tirage. La formule de Poisson permet justement de calculer la probabilité pour qu’une couleur sorte 0 fois, 1 fois, 2 fois … k fois dans un tirage :

D exprime la densité moyenne d’événements. Ici, comme on sort 12 boules chaque tirage, la densité moyenne de l’événement « boule rouge sortie » est donc de 1 fois par tirage ou unité de temps, soit D = 1. Quelle est la probabilité que dans un tirage la boule rouge sorte 0 fois ? P(O) = 0,367 , soit 36.7 % de chances. Pour qu’elle sorte 1 fois ? P(1 ) = 0.367, soit autant de chances. Pour 2 fois? P(2) = 0.183 soit 18.3 % de chances: la probabilité est déjà plus faible. Ensuite, elle diminue rapidement: P(3) = 0.063, P(4) = 0.015.

En remplaçant les boules par des notes, cela pourrait donner, pour que la disposition relève strictement du hasard, l’équivalence suivante: si chaque unité de temps (une mesure par exemple) contient 12 notes, et que l’on se sert du total chromatique, une note donnée, sur 100 mesures (ceci dit pour simplifier), devra apparaître 0 fois dans 36 mesures, 1 fois dans 36 autres mesures, 2 fois dans 18 mesures, 3 fois dans 6 mesures, etc.” (Laurent Fichet).

D’après Gustavo Diaz, la distribution de Poisson est particulièrement utile avec les grandes masses de sons. Par exemple, compte tenu d’une masse de sons avec une densité moyenne de 3 sons par seconde, quelle est la probabilité d’une densité de 5 sons par seconde ? La formule de poisson permet de déterminer que c’est aux alentours de 0,1 :

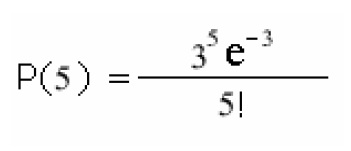
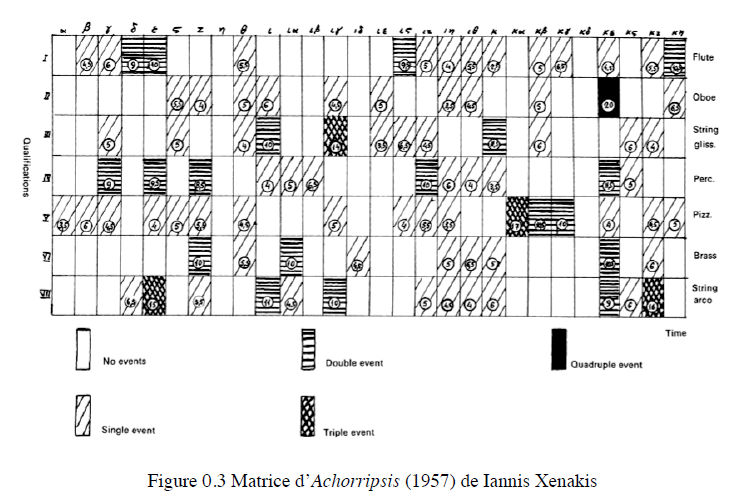
Laurent Fichet relève aussi que la loi de Poisson n’a cependant pas été conçue d’après un modèle perceptif, et ne saurait garantir une “impression” de hasard. C’est cependant dans ce but qu’elle est utilisée par Xenakis dans Achorripsis. La matrice dans laquelle Xenakis répartit les événements musicaux (0 = silence, 1, 2, 3 = groupes de notes) se veut aléatoire. La loi de Poisson lui permet de calculer le nombre d’apparitions sur 196 unités, elles-mêmes réparties sur 7 couches de timbres superposées, mais la répartition des événements dans le tableau tient davantage d’une décision délibérée du compositeur. En effet, la formule de Poisson indique combien d’unités doivent contenir 1 événement donné, combien doivent contenir 2, etc., mais ne fournit aucune indication sur la répartition de ces événements :


Pistes de lecture

 

(Illustration : Graham Holt, Dice, CC-BY-NC)