Automates cellulaires

Les automates cellulaires furent inventés à la fin des années 1940 par Stanislaw Ulam et John Von Neumann, qui s’intéressaient respectivement à la modélisation de la croissance des cristaux et à la capacité d’une machine à s’auto-reproduire.

Pour créer un automate cellulaire, il faut deux éléments :

  • une grille, ou matrice en 1, 2 ou 3 dimensions, où chaque cellule peut connaître un nombre fini d’états (au minimum 2)
  • une règle qui définit l’évolution de chaque cellule lors de l’itération suivante, en fonction de l’état des cellules voisines

A. Wuensche et M. Lesser donnent la définition suivante des automates cellulaires : “Un automate cellulaire est un système discret dynamique qui évolue par itération d’une règle déterministe simple.”

En partant d’une configuration initiale de cellules (la génération 0), on applique les règles, ce qui donne lieu à une nouvelle configuration, sur laquelle les règles peuvent à nouveau s’appliquer, et ainsi de suite. En fonctions des règles, certains automates peuvent donner lieu à des motifs très complexes, et d’autres s’éteindre rapidement. Beaucoup d’automates cellulaires montrent une “propagation de motifs” qui se répète à travers le maillage. C’est notamment cette caractéristique qui rend les automates cellulaires intéressants d’un point de vue compositionnel.

Les règles

Dans l’état le plus simple, une case ne peut connaître que deux états : vivant (1) ou mort (0). D’autres versions plus complexes prévoient plusieurs états pour une même case.

Les automates cellulaires peuvent être à :

  • 1 dimension (cellules disposées sur une ligne, une ligne correspond à une génération)
  • 2 dimensions (cellules disposées sur une grille, une grille correspond à une génération)
  • 3 dimensions (cellules disposées sur une matrice cubique)

Les automates cellulaires à plus de 2 dimensions étant difficiles à visualiser, ils ne seront pas évoqués ici.

Les règles peuvent prendre en compte un nombre plus ou moins grand de cellules avoisinantes. Dans le voisinage dit “von Neumann”, on considère qu’une cellule a 4 voisines (nord sud, ouest, est) :

Dans le voisinage de Moore, il y en a 8 :

On peut aussi parler de voisinage de Moore étendu, lorsque plusieurs rangées autour sont concernées (radius 2, radius 3, etc.).

Pour les automates à 1 dimension, les voisinages de Moore et von Neumann sont identiques:

v c v

Exemple de Moore étendu (radius 2) à 1 dimension :

v v c v v

Les règles déterminant le comportement dynamique d’un système peuvent être classés en 2 catégories :

  • l’état d’une cellule donnée est déterminé en examinant chaque cellule voisine indépendamment
  • l’état d’une cellule donnée est déterminée par la somme des états de ses cellules voisines (règle totalistique)

Les automates à 1 dimension sont décrits par Stephen Wolfram en 1982. Seules 256 règles sont possibles. Pour numéroter chaque règle, on utilise le codage en binaire. Les 8 configurations de voisinages possibles sont codées, puis le résultat donne le nom à la règle. Par ex, on parle de règle 103 :

111 110 101 100 011 010 001 000
0 1 1 0 0 1 1 1

Soit 01100111 (base 2) = 103 (base 10)

Ou (01100111)2 = (103)10

Un automate cellulaire en 1 dimension se développe sur une chaîne continue. Mais pour bien le visualiser, on le présente généralement avec une génération par ligne (ex site Wolfram Alpha).

Une cellule située en bout de ligne est considérée comme voisine de celle du début (géométrie circulaire, ou Tore à une dimension).

Certaines règles donnent des fractales (règle 90 par ex).

Le site Wolfram Alpha permet de tester les différentes règles pour les visualiser.

Classification de Wolfram

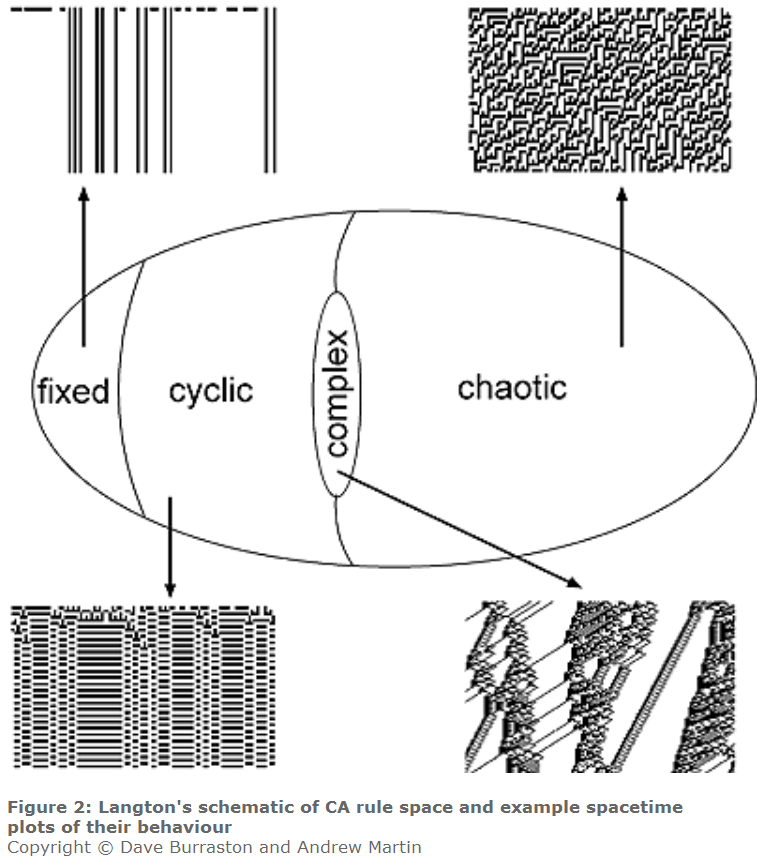
Wolfram classe le comportement des automates cellulaires en 4 classes :

  1. stable : au bout d’un certain nombre de génération, la même configuration se répète à l’infini
  2. cyclique : automate évoluant vers un état stable où les même motifs se répètent périodiquement
  3. chaotique : le système génère des motifs chaotiques et apériodiques, parfois avec des courbes fractales
  4. complexe : comportement complexe mais pas chaotique

D’autres tentatives de classifications existent cependant. C. G. Langton propose quant à lui d’envisager ces différents états comme un continuum :

Les différentes notations

Il importe également d’être familier des différentes manières de coder les grandes catégories d’automates cellulaires, qui sont utilisés par les différents logiciels et applications sur les AC.

La notation de Stephen Wolfram :

  • d = nombre de dimensions
  • k = nombre d’états possibles pour une cellule
  • r = radius de voisinage depuis la cellule évaluée

Par exemple, un automate à 1D k2 r2, signifie que l’automate se déroule sur une ligne (1D), qu’une cellule ne peut connaître que 2 états (k2) et que le radius de voisinage est de 2 cellules depuis la cellule évaluée (r2).

La notation d’Andy Wuensche :

  • v = nombre d’états possibles pour une cellule
  • k = nombre de cellules voisines prises en compte
  • n = nombre d’itérations

La notation « R,W,H » de Mirek Wojtowicz (pour les automates binaires à 2 dimensions) :

  • R = largeur du voisinage pris en compte (range)
  • W = codage de la règle par Stephen Wolfram en valeur hexadécimale (base 16).
  • H (optionnel) =  nombre d’états

En musique

Les automates cellulaires étant un processus qui se développe dans le temps, c’est tout naturellement que des applications musicales ont été rapidement imaginées, dès la fin des années 1980.

Le musicien le plus célèbre ayant utilisé les automates cellulaires est sans doute Iannis Xenakis, dans sa pièce pour orchestre Horos (1986). Le mapping est basé sur des hauteurs pré-déterminées et l’état de la cellule détermine le choix de l’instrumentation ; les événements musicaux sont contrôlés par la présence ou l’absence de cellule.

L’auteur de science-fiction Rudy Rucker appelle “Gnarl” l’état idéal entre aléatoire chaotique et prédictible en art. Il suggère que les automates cellulaires décrits par Stephen Wolfram sont un outil de compréhension du “Gnarl”. Paul D. Reiners parle particulièrement du “Gnarl” à propos de la règle 225.

Mapping “piano-roll” de Stephen Wolfram

C’est le mapping musical le plus simple des automates cellulaire. Il consiste à définir une bande au milieu de l’automate et à retourner virtuellement la matrice à l’horizontale :

Puis interpréter le résultat comme un piano-roll midi (hauteurs en ordonnées, durées en abscisses, les cases actives adjacentes étant lues comme un son tenu).

Cette technique produit des accords denses, mais la récurrence des motifs est clairement audible.

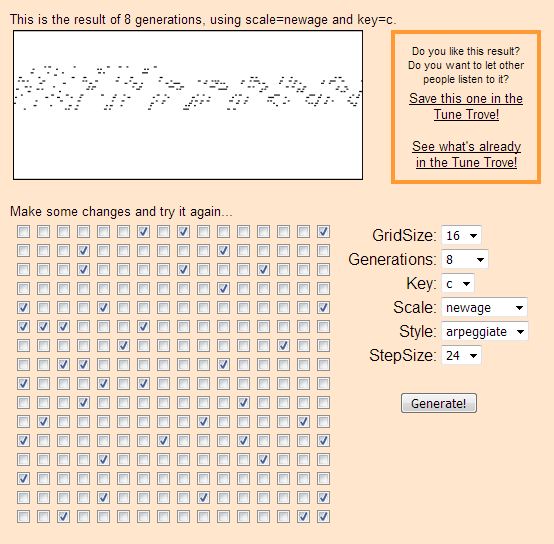
Un système assez similaire est proposé par Tim Thompson dans l’un de ses “TuneToys”, “Life forms”. Comme son nom l’indique, il s’agit d’un générateur basé sur le Jeu de la Vie. La matrice à 2 dimensions y est considérée comme un piano-roll vierge : l’utilisateur est invité à noircir certaines cases, ce qui a pour effet de créer une phrase initiale. Chaque génération suivante crée une variation de cette première phrase :

(Samples : Sonatina Symphonic Orchestra, Creative Commons CC-BY)

(Samples : Samulis – Marimba Samples, Freesound, Creative Commons CC-BY)

Mapping de Eduardo R. Miranda (logiciel CAMUS)

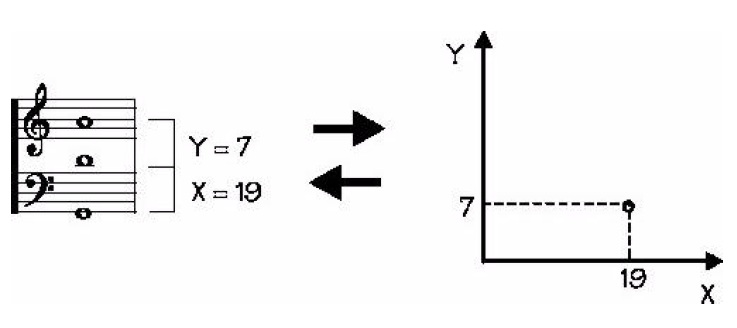
Automates cellulaires à 2D (Jeu de la vie de Conway), pour générer des hauteurs et des durées.

Chaque cellule active fournit ses coordonnées et permet donc de générer une triade (dans l’exemple ci-dessous, le sol grave est pris comme repère-origine) :

Les autres données (ordre dans lequel les 3 notes sont jouées et durées) sont produites par des listes de bits générés à partir des 8 cellules avoisinantes :

Ce qui donne 4 listes intitulées de w1 et w4

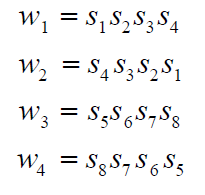
Pour l’organisation temporelle (triggering time), on combine les liste w1 et w2 par opérateur OU inclusif. Pour les durées, w3 et w4.

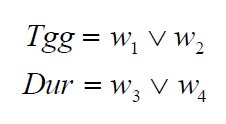
Par exemple :

w1 = 0111

w2 = 1110

w1 V w2 = 1111

Puis on cherche la configuration de synchronisation dans le tableau de correspondance ci-dessous :

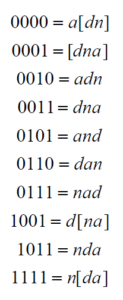
Ce qui permet de donner les possibilités de synchronisation suivantes (AND : du grave à l’aigu, quand deux notes sont entre crochets, elles sont jouées en même temps) :

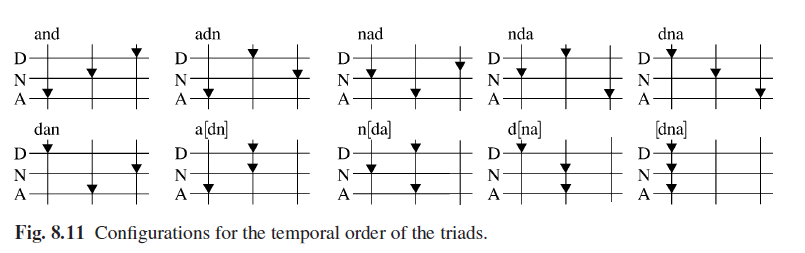
Exemple de configuration NAD :

Pour générer la durée, le processus est le même, mais cette fois-ci, c’est le moment d’extinction du son qui est déterminée par la matrice AND :

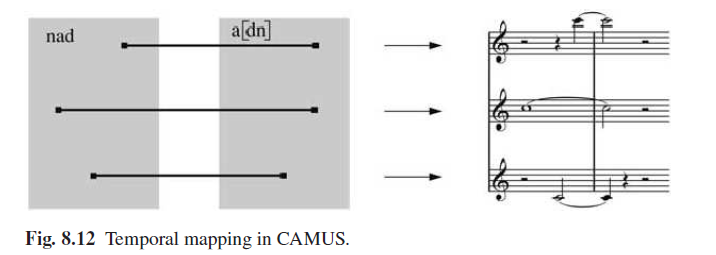
Mapping de Gustavo Diaz

Proposition de mapping de Gustavo Diaz pour un automate cellulaire à 1 dimension : établir une correspondance pour chaque configuration possible sur une génération. Pour cela, il faut coder chaque configuration possible.

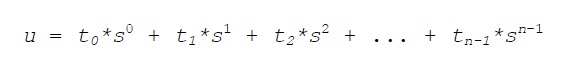
s = nombre d’états possibles pour une cellule
n = nombre de cellules sur la grille (de 0 à n-1)
t base p = état d’une cellule en position p (p de 0 à n-1)

Autrement dit, pour chaque génération, noter les cases vivantes, puis pour chaque cellule vivante, calculer 2 puissance rang de la case, la première étant 0.

Puis modulo 24 entre do4 et ré5
64 cases
320 générations
1 note = 1 génération

Exemple donné par Gustavo Diaz :

Diaz indique notamment que les règles de classe 4 lui semblent les plus fécondes en musique, point de vue bien sûr réfutable si l’on préfère envisager les automates cellulaires pour leur sérendipité et leur comportement chaotique.

Exemples de compositions d’après les automates cellulaires

Pistes de lecture

 

(Illustration : hawkexpress, Cellular Automaton : Rule 45, CC-BY-NC-ND)