INDEX
1 – Bruit 1/f
2 – Suite de Thue-Morse
3 – Série infinie de Per Norgard
4 – Mélodies autosimilaires (Tom Johnson)
5 – Pistes de lecture
Bruit 1/f
L’étude de la fonction 1/f en musique part du principe que l’équilibre entre surprise et prédictibilité fait partie des sources du plaisir musical.
Ce qu’on désigne ordinairement par “bruit 1/f” devrait en réalité s’écrire bruit 1/f≃1.
La formule 1/fn fait référence au spectre du bruit. f représente la fréquence et n est compris entre 0 et 2.
- Dans le cas du bruit blanc (1/f0), chaque fréquence est imprévisible. On obtient un spectre uniforme, de même valeur quelle que soit la fréquence.
- Dans le cas du bruit rose (1/f1), qui est donc synonyme de celui généralement désigné par l’expression “bruit 1/f”, le spectre décroît en 1/f (f1 = f). Donc l’amplitude du spectre est divisée par 2 à chaque octave. Le spectre de ce bruit est en filtre passe-bas par rapport au bruit blanc.
- Dans le cas du bruit brownien (1/f2), le spectre décroît en 1/f2. Il y a encore plus de basses fréquences.
Moins le spectre est uniforme (moins il est plat), plus le signal est corrélé, c’est-à-dire qu’il existe des relations de plus en plus fortes entre une valeur du signal et les valeurs précédente.
- Ainsi pour un bruit blanc, chaque valeur du signal est indépendante des précédentes.
- Pour un bruit rose, les relations entre les valeurs ne sont plus totalement aléatoires et sont reliées entre elles sur un intervalle de temps court, comme si l’on jouait des notes aléatoires sur un clavier mais sans pouvoir s’éloigner trop des notes précédentes.
- Pour le bruit en 1/f2, la corrélation est encore plus fortes. Les notes sont aléatoires mais doivent être reliées à de nombreuses notes précédentes.
Plus l’exposant n est grand, plus la relation entre les valeurs aléatoires est forte. Le cas limite se produit lorsque le spectre est nul partout sauf pour une fréquence : c’est le spectre d’une sinusoïde. En ce cas, chaque valeur du signal est entièrement déduite des précédentes et il n’y a plus d’aléatoire.
Dans un article paru dans les années 1970, les chercheurs Richard Voss et John Clarke analysent la densité spectrale d’enregistrements de musique (jazz, classique, rock…), et découvrent qu’elle se situe à mi-chemin entre le bruit blanc (1/f0) et le bruit brownien (1/f2). Ils firent ensuite l’expérience inverse, c’est-à-dire générer de la musique avec ces 3 différents bruits, en mappant le résultat sur deux octaves d’une échelle musicale et en appliquant le même procédé pour la durée des notes. En faisant écouter le résultat à des auditeurs, ces derniers jugèrent que la musique obtenue par bruit blanc était trop aléatoire, celle brownienne trop prévisible, celle 1/f1 semblait de la musique « normale ».
Exemple de mélodie chromatique aléatoire (mappée sur 16 hauteurs entre si3 et ré4) :
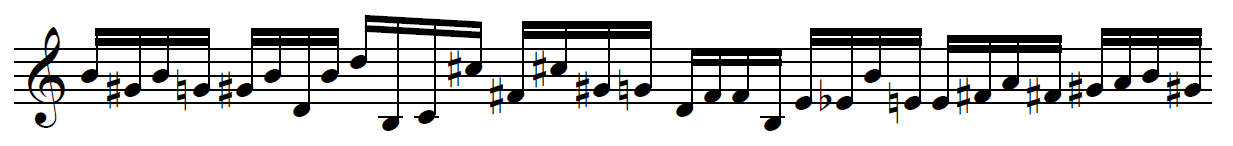
Exemple de mélodie chromatique brownienne (même mapping) :
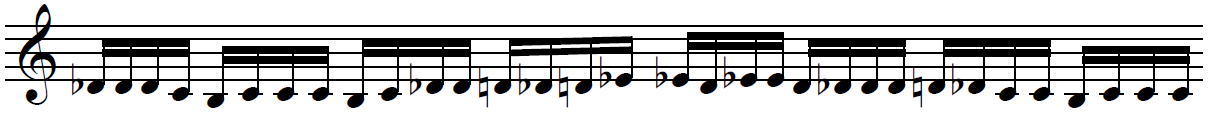
Exemple de mélodie chromatique “1/f” (même mapping) :

Télécharger le patch Pure data (distribution Purr Data – anciennement Pd-Extended) ![]()
Benoît Mandelbrot, qui qualifie la distribution 1/f de “fractale”, explique simplement ce phénomène :
« L’argument que je favoriserais est que les compositions musicales sont, comme leur nom l’indique, composées : d’abord, elles sont subdivisées en mouvements caractérisés par leur tempo et/ou leur niveau d’intensité global, puis chaque mouvement est subdivisé à son tour de la même manière. (…) Le résultat est destiné à présenter des propriétés gigognes.”
Comment simuler bruit blanc, browniens et 1/f sans ordinateur ?
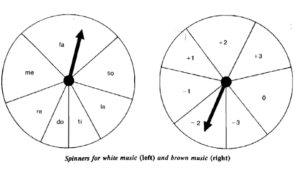
(image extraite de l’article de Martin Gardner sur les bruits fractals)
- Bruit blanc : jeter un dé pour définir chaque nouveau son
- Bruit brownien : lancer une pièce à pile ou face, faire monter le son sur face, le faire descendre sur face.
- Bruit 1/f :
- réunir 3 dés classiques (à 6 faces), de couleurs différentes : bleu, vert et rouge
- tracer un tableau où l’on note les nombres de 0 à 7 en notation binaire, en assignant une couleur à chaque colonne, comme suit :
| Index | Bleu | Vert | Rouge | |
| 0 | 0 | 0 | 0 | Tous les dés sont jetés. |
| 1 | 0 | 0 | 1 | Le dé rouge est jeté |
| 2 | 0 | 1 | 0 | Les dés verts et rouges sont jetés |
| 3 | 0 | 1 | 1 | Le dé rouge est jeté |
| 4 | 1 | 0 | 0 | Tous les dés sont jetés |
| 5 | 1 | 0 | 1 | Le dé rouge est jeté |
| 6 | 1 | 1 | 0 | Les dés verts et rouges sont jetés |
| 7 | 1 | 1 | 1 | Le dé rouge est jeté |
- La 1ère note de la mélodie est déterminée en jetant les 3 dés et en prenant la somme, ce qui donne un résultat entre 3 et 18, qui seront assignés aux 16 touches adjacentes d’un clavier. Le premier résultat correspond au stade zéro.
- Pour chaque nouveau jet de dés, consulter le tableau et identifier quelle(s) colonne(s) changent dans la notation binaire. Ainsi, en comparant la ligne 0 et 1, on s’aperçoit que seule la valeur du dé rouge change. On jette alors uniquement le dé rouge, et on additionne le résultat aux dés restés immobiles. A la ligne suivante, c’est la valeur de la colonne verte et rouge qui change, on lance alors les dés verts et rouge, et ainsi de suite.
Loi de Zipf
La légende voudrait que le linguiste George Kingsley Zipf (prononcer “Zif”), entreprenant l’analyse lexicale de Ulysse de Joyce pour y étudier la récurrence des mots, aurait mesuré que:
- le mot le plus courant revenait 8 000 fois ;
- le dixième mot le plus fréquent revient 10x moins souvent que le plus courant ;
- le centième, 100X mois souvent ;
- le millième, 1000X mois, etc.
Zipf a également travaillé sur des corpus littéraires et musicaux, en petite quantité car il faisait le travail à la main.
La loi de Zipf prévoit que dans un texte donné, la fréquence d’occurrence f(n) d’un mot est liée à son rang n dans l’ordre des fréquences par une loi de la forme f ( n ) = K / n où K est une constante. La fréquence d’emploi du n-ième mot le plus employé d’une langue varie en 1/n. Ses travaux peuvent être utilisés pour étudier les propriétés statistiques de grands ensembles de données.
En physique, la loi de Zipf est un cas particulier des lois de puissance. Lorsque n = 1 (l’idéal de Zipf), le phénomène est appelé bruit 1/f (ou bruit rose).
H.A. Simon a ainsi tenté de donner une explication à cette loi : “L’hypothèse basique serait que, lorsque des mots sont ajoutés successivement à une texte, ils créent un contexte.” Comme ce contexte émerge, il favorise l’apparition de certains morts, en particulier ceux qui sont déjà apparus, met l’accent sur certaines catégories de noms et d’adjectifs, le choix des temps, et limite l’utilisation des autres.
En musique, le contexte est déterminé par une hiérarchie de motifs entremêlés à différentes échelles de temps : au niveau mélodique (répétitions, variations, modulations) et à plus grande échelle, où la récurrence de longues sections et certaines progressions harmoniques standard détermine la forme musicale.
Appliquer la loi de Zipf au domaine musical ne va cependant pas de soi ; en effet, il n’y a pas d’équivalence évidente entre le mot et un concept musical. On peut choisir de considérer comme mot une note avec sa durée et sa hauteur spécifique. Cela reste en-dessous du nombre de mots du vocabulaire utilisé dans un texte, mais permet une marge statistique suffisante. Avec cette hypothèse, la comparaison de plusieurs pièces tonales permet d’observer la loi de Zipf sur la musique tonale, beaucoup moins sur la musique atonale.
Suite de Thue-Morse
La suite de Thue-Morse est une suite binaire. On peut la construire directement avec un algorithme très simple.
Jouer une note et son opposé : 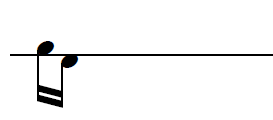
Jouer le groupe de 2 notes ainsi obtenu et son renversement : 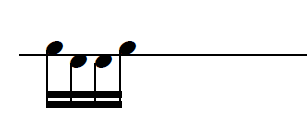
Jouer le groupe de 4 ainsi obtenu et son renversement : 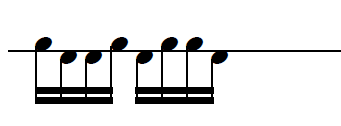
Et ainsi de suite : 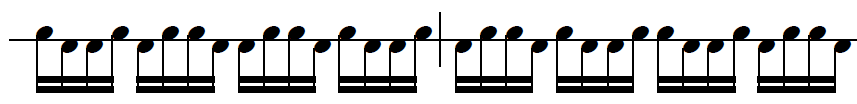
On peut visualiser ainsi le déroulement de l’algorithme (source de l’animation : Wikimedia Commons) :

Il est également possible d’obtenir la série de Thue-Morse en traduisant la série des nombres naturels (0, 1, 2, 3, 4…) en nombres binaires, puis en en calculant la racine numérique et la réduisant en modulo 2 :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | … |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | … |
Cette série a été imaginée initialement pour ne présenter aucune répétition de plus de deux valeurs consécutives.
Elle possède des propriétés fractales. Si l’on supprime tous les termes impairs, la série reste inchangée :
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 …
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 …
On obtient le même résultat en retirant des paires :
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 …
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 …
Cette série en apparence simple est utilisée telle quelle par Per Norgard dans sa 3e symphonie et I Ching pour percussions.
Gustavo Diaz propose quant à lui une musicalisation à plus de 2 termes en passant par la construction non-récursive de la série (par les nombres binaires). Il s’agit de traduire la série des nombres naturels en nombres binaires, puis d’additionner :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | … |
| 0 | 1 | 1 | 2 | 1 | 2 | 2 | 3 | 1 | … |
En mappant le résultat, par exemple sur 2 octaves chromatiques, on obtient une mélodie qui a les mêmes propriétés fractales (identique à elle-même si on supprime les termes impairs, etc.).
On obtient des résultats intéressants en multipliant les nombres naturels par un nombre constant. Par exemple avec 17 :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 0 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | … |
| 0 | 10001 | 100010 | 110011 | 1000100 | 1010101 | 1100110 | 1110111 | 10001000 | … |
| 0 | 2 | 2 | 4 | 2 | 4 | 4 | 6 | 2 | … |

Le même exemple généré avec le logiciel FractMus (base 2, multiplicateur 17), mappé en mode à transposition limité n°2 de Messiaen :

Pour explorer ces différentes possibilités, on peut recourir au logiciel gratuit FractMus, qui ne propose pas la version originelle, donc binaire, de la suite de Thue-Morse, mais uniquement ses versions non-récursives. Pour obtenir d’autres résultats, on peut garder la série des nombres naturels, mais la traduire en base 3, et la multiplier : plus la base est élevée, plus les écarts sont importants.
Gustavo Diaz note que certains rapports entre la base et le multiplicateur donne des résultats mélodiques plus intéressants que d’autres, notamment :
- base n et multiplicateur nk 1, où k = {1, 2, 3, 4…)
- base n et multiplicateur n! k, où k est proche de n (ceci vaut uniquement pour les petites bases)
Série infinie de Per Norgard
Cette série a été inventée par Per Norgard en 1959. Elle lui sert de matériau thématique dans plusieurs de ses oeuvres : Voyage into the Golden Screen, Iris, Symphonie no 2. L’objectif est de générer une suite de note ni trop aléatoire ni trop prévisible, et restant dans un ambitus exploitable autour d’une note initiale. Sur le site web du compositeur (aujourd’hui hors ligne), Jørgen Mortensen décrit plusieurs méthodes pour générer la série infinie. La première est celle de la projection d’intervalle :
L’exemple donné part du sol, mappé dans une échelle chromatique. Notons qu’il est bien sûr possible d’utiliser aussi bien une échelle diatonique, micro-tonale… Le noyau du système est le premier intervalle :

Chacune de ces notes et le point de départ de deux projections :
- la projection “supérieure”, où l’intervalle de référence est inversé
- la projection “inférieure” où l’intervalle de référence est inchangé
Chaque nouvel intervalle se calcule en fonction de la note qui précède sur son propre axe de projection (supérieur, inférieur).
Dans l’exemple, l’intervalle de référence (+1, seconde mineure ascendante) devient donc -1 par rapport à sol (=> fa#) et reste +1 par rapport à lab (=> la bécarre)

Nous avons ainsi deux nouvelles notes, et un nouvel intervalle, entre lab et fa# : une seconde majeure descendante (-2).
Ce qui donne donc avec la même méthode, +2 sur l’axe supérieur (par rapport à fa#) : lab
Et -2 sur l’axe inférieur (par rapport à la) : sol

Et ainsi de suite :

(Samples : Sonatina Symphonic Orchestra, Creative Commons CC-BY)
Méthode binaire :
Cette technique pourrait sembler plus anecdotique, mais elle a pour intérêt de permettre de déterminer quel note correspondra à un moment n de la série, sans avoir à la construire pas à pas.
On remplace les chiffres de rang par leur équivalent en notation binaire. Pour obtenir le nombre correspondant dans la série de Norgard, on lit le nombre de la gauche vers la droite, en inversant la polarité à chaque 0.
| Ex : 5 | ||
| 101 | ||
| 1, puis -1, +1 = 0 |

Per Norgard se sert de cette série pour générer du matériau mélodique, et non pas pour l’étendre aux autres paramètres musicaux (durées, dynamiques) comme l’aurait voulu la pensée sérielle à cette époque. Pour décrire les saisissantes propriétés fractales de cette série, Norgad emprunte à Arthur Koestler (Au delà du réductionnisme) le concept de “hiérarchie ouverte” : un système où les différentes couches sont connectées structurellement, mais où aucune couche n’est finalement supérieure à une autre.
En effet, la série garde son identité même si l’on supprime une note sur 4 ou sur 16. Sa forme se manifeste simultanément à des échelles différentes (invariance d’échelle et autosimilarité).

En choisissant de faire entendre seulement une note sur 3, ou sur 5 (le compositeur parle de “longueur d’onde” de 3, 5, etc.), Norgard donne naissance à de nouvelles séries infinies possédant les mêmes caractéristiques hiérarchiques, bien que différentes de celles de la série originale :

Quel rapport avec Thue-Morse ?
En fait, on peut considérer la suite de Thue-Morse comme une série infinie de Norgard comportant seulement 2 éléments. Pour la réduire à deux éléments (0 et 1), il faut :
- lorsque la valeur excède 1, soustraire 2 (ou 4, ou 8, etc., selon ce qui est nécessaire pour obtenir 1 ou 0
- lorsque la valeur est en dessous de 0, additionner 2 (ou 4, ou 8, etc.).
Le résultat est la série de Thue-Morse :
| 0 | 1 | -1 | 2 | 1 | 0 | -2 | 3 | -1 | 2 | 0 | 1 | 2 | -1 | 3 | 4 | 1 | 0 | -2 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
Mélodies autosimilaires (Tom Johnson)
Une mélodie autosimilaire coïncide avec elle-même lorsqu’elle est jouée à un tempo plus lent.
Dans son livre “Self-similar Melodies”, Tom Johnson décrit plusieurs algorithmes permettant de générer des mélodies de ce type.
L’un des plus simples est le suivant :
n n+1 n-1 n
Soit, avec n=1 :
1 2 0 1
Pour poursuivre la série, il suffit de refaire l’opération en partant de la deuxième note de la série ainsi obtenue (ici, 2), et ainsi de suite.
On obtient pour commencer :
1 2 0 1 2 3 1 2 0 1 -1 0 etc.
Jouée rapidement sur une échelle chromatique, la série produit une mélodie très “vol du bourdon”, autosimilaire à un ratio de 1 : 4 :

Pistes de lecture
- Per Norgard, Inside a Symphony
- Algorithmic Composer : Tom Johnson’s Self Similar Melodies
(Illustration : Justin Lincoln, CC-BY-SA)