INDEX
1 – Historique
2 – Fonctionnement
3 – Chaînes de Markov d’ordre n
4 – Exemples d’utilisation en musique
5 – Marches markoviennes
6 – Chemins hamiltoniens
7 – Pistes de lecture

Historique

Les chaînes de Markov doivent leur nom à un mathématicien russe qui a consacré l’essentiel de ses travaux à l’étude des probabilités. En 1913, il fit une analyse statistique des lettres utilisées dans le roman de Pouchkine “Eugène Onéguine” qui lui permit de formaliser par des graphes la manière dont la probabilité d’un événement est fortement conditionnée par les événements qui le précèdent.

Fonctionnement

Une chaîne de Markov permet de déterminer l’état suivant en fonction de l’état actuel et d’un jeu de probabilités. Prenons pour l’illustration l’air “Ah vous dirai-je maman” :

L’analyse de la chanson permet de déterminer quelles probabilités chaque note a d’être suivie de telle ou telle autre :

C : C, G, G

D : D, C, G, C

E : E, D, E, E, D, E, E, D

F : F, E, F, E, F, E

G : F, G, F, G, F

A : A, G

On mesure la probabilité par une valeur entre 0 et 1. Ainsi, la probabilité que la soit suivi d’une autre la est de 0,50.

En reportant ces valeurs, dans un tableau, on obtient ce qu’on appelle une Matrice de transition.

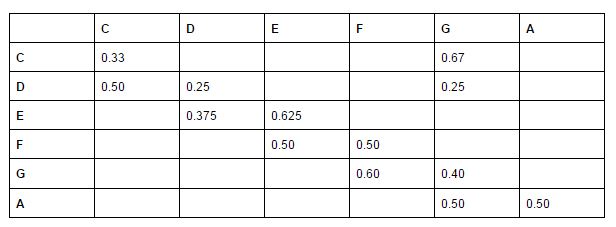
Un processus semblable peut être appliqué aux durées :

Ces deux tables permettent de générer une ligne mélodique basée sur les probabilités de la mélodie analysée (en bleu, les segments de plus de trois notes similaires à l’original) :

(On remarque au passage que cette technique est peu adaptée à l’imitation des rythmes mesurés.)

Chaînes de Markov d’ordre n

On parle de chaîne de Markov d’ordre 0 lorsque le choix s’effectue en tenant uniquement compte de l’état actuel (“phénomène aléatoire à mémoire courte”), d’ordre 1, si la sélection se fait en fonction de l’état actuel et de l’état précédent, et ainsi de suite. Ainsi, en poursuivant l’exemple de “Ah vous dirais-je maman” :

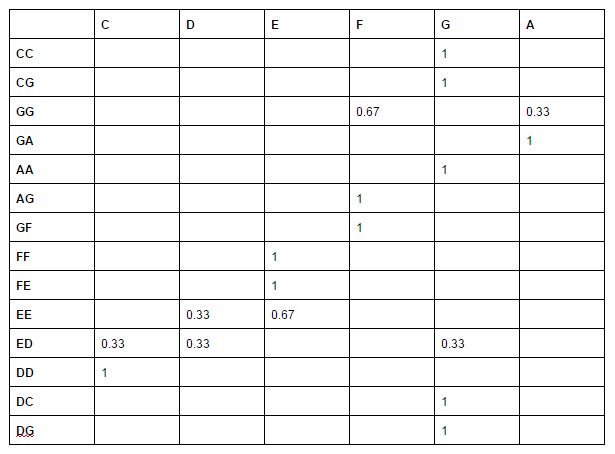
Ce qui permet de générer une mélodie plus proche encore de l’originale :

Le problème est que, plus on prend en compte d’états précédents (2e ordre, 3e ordre et au-delà), plus le risque de générer des segments entiers semblables à l’original grandit exponentiellement (dans le cas de notre exemple, la simplicité et la dimension répétitive de la comptine accélère le processus). C’est ce que François Pachet appelle « Max Order Problem ». Dans une optique d’imitation stylistique, il y a donc un équilibre à trouver entre les résultats souvent décousus produits par les chaînes de Markov de premier ordre, et le plagiat pur généré par des chaînes de Markov d’ordre supérieur à 4.

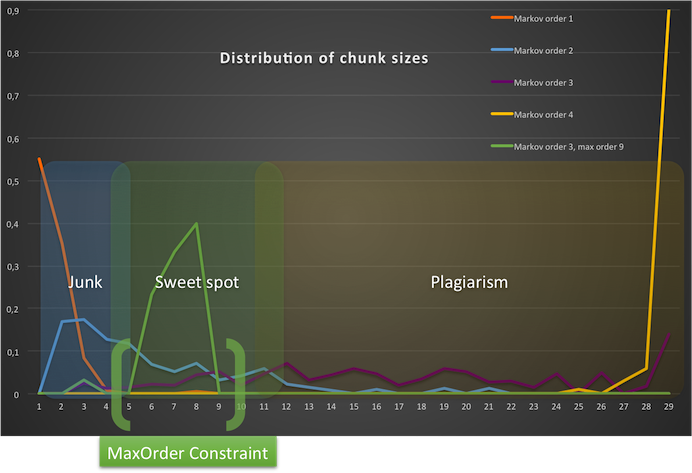
Exemples d’utilisation en musique

Les chaînes de Markov sont un outil simple et puissant, pouvant être appliqué aux hauteurs, aux intervalles, aux accords, aux durées, et capable d’un grand nombre d’applications (voir par exemple l’usage qu’en fait le compositeur Philippe Manoury pour la musique électronique en temps réel). Leur principale limite est qu’elles ne capturent pas des structures. Ainsi, dans le domaine mélodique, elles ne permettent pas (sauf très accidentellement) de générer des motifs qui se répètent (des marches harmoniques par exemple), à la différence d’outils tels que les fractales, ni de générer de cadences à des points précis du processus, comme avec les grammaires génératives.

L’exemple le plus simple d’utilisation des chaînes de Markov est la génération d’un flux mélodique. Hiller et Isaacson, qui furent les premiers à utiliser les chaînes de Markov dans une composition musicale (dans la Suite ILLIAC), l’utilisent dans les Expériences 3 et 4 dans le cadre d’une imitation de la musique tonale. Dans Initiation à la composition musicale automatique, Pierre Barbaud propose quant à lui une matrice de transition harmonique correspondant au mode majeur (l’accord mineur de 3e degré est remplacé ici par un accord parfait majeur emprunté au ton relatif mineur) :

	I	II	III M	IV	V	VI
I		0.20	0.02	0.40	0.25	0.13
II	0.14		0.50	0.01	0.30	0.05
III M		0.27				0.73
IV	0.24	0.02			0.72	0.02
V	0.77	0.02	0.01	0.10	0	0.10
VI	0.01	0.90	0.04	0.03	0.02

Il est ensuite possible de générer une réalisation polyphonique des accord en question, en respectant la “règle des indices” (La musique, discipline scientifique, p.51) : si la basse monte d’une 2nde, tierce ou quarte, alors le comportement des 3 autres voix est le suivant :

	5	3	(la quinte du 1er accord devient la tierce du suivant)
	3	0	(la tierce devient la fondamentale)
	0	5	(la fondamentale devient la quinte

Si la basse descend d’une 2nde, tierce ou quarte, alors :

	5	0
	3	5
	0	3

Notons au passage que la “règles des indices” de Barbaud rappelle fortement la table proposée par Thomas Campion (1567 – 1620) dans son traité de contrepoint :

Une autre méthode fréquemment utilisée est de générer une matrice de transition à partir de l’analyse d’une pièce donnée (comme on peut s’y exercer avec ces abstractions Pure Data de Gérard Paresys).

Les marches markoviennes

Les marches markoviennes (random-walk) sont un cas particulier de chaîne de Markov : dans un tel système, on ne peut passer d’un événement e1 qu’aux événements immédiatement adjacents e1 +1 ou e1 – 1.

Autrement dit, la matrice de transition présente une série de valeurs de chaque côté de la diagonale principale, et des zéros partout ailleurs (on note au passage que certaines mélodies, privilégiant les degrés conjoints, comme l’air “Ah vous dirai-je maman” examiné plus haut, présentent une matrice d’un profil assez similaire). Par exemple :

	1	2	3	4	5
1		1
2	.5		.5
3		.3		.7
4			.6		.4
5				1

Cette technique est adaptée aux processus sonores demandant des changements d’incrémentation fine et progressive. Dans le deuxième mouvement de sa pièce algorithmique Macricisum (1977), “Cosmic Wind Harp”, le compositeur Kevin Jones superpose 20 marches markoviennes au 20ème de seconde entre des partiels adjacents, sur une séquence de fondamentales changeant aléatoirement.

Les chemins hamiltoniens (Michel Philippot)

Inventé par le compositeur français Michel Philippot qui l’utilisa notamment dans son deuxième quatuor à cordes, les chemins hamiltoniens sont une technique d’exploration systématique d’une suite mélodique, permettant au compositeur d’avoir une vision globale sur l’ensemble des enchaînements intervalliques possibles à partir d’un matériau de base.

Soit par exemple la série mélodique issue du thème de la Musique pour cordes, percussion et célesta de Bartok :

On dresse ensuite un tableau qui s’apparente à une matrice de transition markovienne, sauf qu’ici on note seulement si une note est suivie d’une autre, sans préciser de pourcentage.

	do	do#	ré	ré#	la	la#	si
do							X
do#	X		X
ré				X
ré#	X
la						X
la#		X			X	X
si

Puis on liste les couples possibles :

c – b
c# – c
c# – d
d – d#
a – a#
a# – c#
b – a
b – a#

Puis les triplets :

c – b – a
c – b -a#
c# – c – b
c# – d – d#
etc.

Cette technique permet de visualiser les potentialités d’une série de manière exhaustive.

Pistes de lecture

• Algorithmic Composer – Markov Chains in PureData
• Philippe Manoury, Les Chaînes de Markov… à l’infini

 

(Illustration : chrstphré cæmpbëll, RailsTwo(g, CC-BY)