Fractales

L’itération

Pour obtenir une série chaotique ou fractale, on applique ce qu’on appelle l’itération, c’est-à-dire la répétition d’une opération sur une valeur de départ en ajoutant le résultat à la fin de la liste. A chaque itération, on reprend la dernière valeur obtenue et on lui applique la même opération, un nombre n de fois. En programmation, on peut aussi parler de récursivité.

Mathématiquement, on note cette opération : n+1=F(n).

Suite de Syracuse

La suite de Syracuse (ou suite 3n+1, ou Hailstone Sequence en anglais) s’obtient par l’algorithme suivant : on part d’un nombre entier plus grand que zéro ; s’il est pair, on le divise par 2 ; s’il est impair, on le multiplie par 3 et on ajoute 1. En répétant l’opération, on obtient une suite d’entiers positifs dont chacun ne dépend que de son prédécesseur.

Par exemple, à partir de 9, on construit la suite des nombres : 9 – 28 – 14 – 7 – 22 – 11 – 34 – 17 – 52 – 26 – 13 – 40 – 20 – 10 – 5 – 16 – 8 – 4 – 2 – 1… C’est la suite de Syracuse du nombre 9.

En l’état actuel des recherches, il semble que toutes les suites de Syracuse se terminent tôt ou tard par la boucle : 4,2,1,4,2,1,4,2,1…

Le nombre de départ qui donne la plus longue série est 27.

En mappant le résultat avec un modulo 12 (échelle chromatique), on obtient par exemple :

Suite de Syracuse du nombre 9 (visualisation obtenue avec le logiciel FractMus) :

(Samples : Sonatina Symphonic Orchestra, Creative Commons CC-BY)

Suite de Syracuse du nombre 54 :

Suite de pliage de papier

La suite de pliage de papier, aussi appelée suite de la courbe du dragon, résulte de l’expérience la plus simple qui soit : pliez une feuille de papier plusieurs fois consécutives, toujours dans la même direction. En dépliant la feuille et en observant la direction des plis successifs sur la tranche de la feuille, une séquence binaire apparaît (D = droite, G = gauche) :

G G D G G D D G G G D D G D D G G G D G G D D D G G D D G D D etc.

Le physicien John E. Heighway, remarqua que la courbe ainsi obtenue, quel que soit le nombre de fois où l’on plie la feuille, présentait toujours plus ou moins le même profil, avec une tête, deux pieds et une longue queue, ce qui l’incita à nommer cette série « courbe du dragon ».

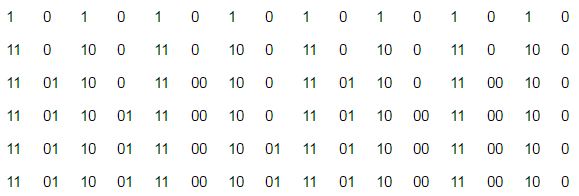
L’une des procédures possibles pour construire la série consiste à partir d’une séquence de 0 et de 1, puis de remplir un intervalle sur deux alternativement par 1 et 0 :

Et de renouveler l’expérience autant de fois que nécessaire :

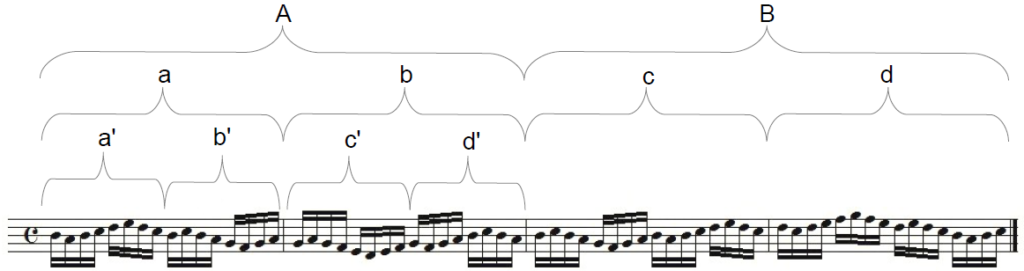
Un moyen simple de sonifier la courbe du dragon, proposé par Tom Johnson dans son livre Self-Similar Melodies, et d’interpréter chaque direction par le sens d’un intervalle musical (montant ou ascendant) :

Tom Johnson fait remarquer que le profil mélodique ainsi obtenu se rapproche de ce qu’une approche intuitive pourrait considérer comme « une belle mélodie » (« Keep the line flowing, make it reach its high point just after the center, let it pass through sequences that will give it a forward motion, let it relax and drop back down at the end of the phrase »).

La mélodie présente en tout cas des propriétés fractales remarquables, puisque la même forme se reproduit à différentes échelles : la deuxième moitié est l’exacte inversion de la première, dont la première moitié est également l’inversion de sa voisine, et ainsi de suite :

Les fractales

Le mot fractale, inventé par Benoît Mandelbrot d’après le latin fractus (fragment, morceau) désigne une forme géométrique (une courbe ou une surface) créée par des règles déterministes et présentant le plus souvent des propriétés d’auto-similarité à toutes les échelles. L’autosimilarité peut être exacte (une partie agrandie de l’objet est identique à l’objet dans son entier) ou statistique (les propriétés statistiques de la partie sont identiques à celles du tout).

Des motifs fractals s’observent fréquemment dans la nature (structure du chou romanesco, vue aérienne de la côte bretonne…), avec des propriétés d’autosimilarité statistique.

Interprétations musicales

Alors que les propriétés des fractales sont aisément appréhendées visuellement, la dimension temporelle propre à la musique semble a priori peu adaptée pour percevoir les fractales.

Ainsi, certains compositeurs n’hésitent pas à interpréter très librement le concept de fractales dans leur musique, comme le fait le musicien brésilien Dmitry Kormann avec sa pièce Coral reef Symphony. S’inspirant de la récurrence des motifs mélodiques dans le Sacre du Printemps de Stravinsky, il met en place une technique sophistiquée de “loops” gigognes.

Dans le Sacre, Stravinsky passe souvent d’un thème A à un thème B en répétant le thème A dans des fragments de plus en courts, interrompus par des fragments de plus en plus longs du thème B (les chiffres représentent le nombre de temps correspondant à chaque motif) :

(schématisation par D. Kormann du “Jeu des Cités rivales”)

En combinant cette technique avec les structures autosimilaires de John Cage dans First Construction (in metal), Kormann met au point l’approche suivante : soit la structure de 12 mesures suivantes, où le motif A occupe les 3 premières mesures, le motif B la 4e mesure, etc.

Si l’on souhaite étendre ce processus à une séquence de deux nouveaux motifs C et D, Kormann propose d’enchâsser les motifs A et B dans une macro-structure Q de mêmes proportions, et d’en faire autant des motifs C et D dans une structure R :

Et ainsi de suite :

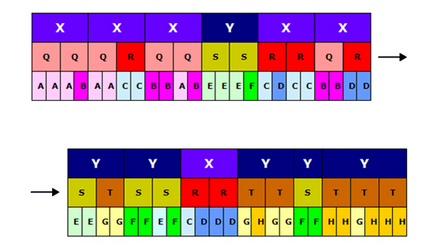
Le compositeur exploite ainsi des logiques fractales pour trouver le moyen le plus fluide de faire évoluer son discours musical, sans que le systématisme de ce jeu de proportions enchâssées soit immédiatement perceptible à l’oreille de l’auditeur attentif.

Plus libre encore, l’approche du compositeur David Clark Little qui développe les principes chaotiques pour l’improvisation, dans une pièce intitulée Brain-Wave, pour au moins 3 musiciens, qui évoque les techniques développées par Vinko Globokar dans ses oeuvres des années 1960 (comme Correspondance) :

“Les interprètes sont assis un peu partout dans une salle de concert, dans une direction arbitraire, et commencent à jouer. Ils suivent un ensemble de consignes qui déterminent ce qu’ils jouent en fonction de ce jouent les autres musiciens assis et où les autres musiciens sont assis par rapport à eux. Globalement, ils essaient d’imiter ce que font les musiciens en face d’eux et de faire l’inverse de ce que font les musiciens derrière eux (par exemple, si le joueur en face d’eux accélère, ils doivent accélérer ; si le joueur derrière eux commence à jouer plus doucement, ils doivent jouer plus fort…). Le titre de la pièce rappelle que ce système est une manière d’imiter le fonctionnement des neurones inhibiteur et excitateurs dans le cerveau humain, dont certains chercheurs ont découvert le comportement chaotique.

Compositions utilisant des fractales

Pistes de lecture

 

(Illustration : Sanchtv, Foldable Fractal 2.0, CC-BY-NC-ND)