Mapping, sonification

Le mapping est le processus permettant de convertir une séquence de données numériques ou symboliques issue d’un algorithme quelconque en données sonores, à l’échelle micro :

hauteur ou intervalle,
durée ou rythme,
dynamique,
paramètre d’enveloppes ou de spectre,
fréquence de filtrage,
paramètres d’un effet,
…

ou macro :

motif,
phrase mélodique,
sample,
…

On peut voir les techniques de cryptogrammes musicaux en usage depuis Guido d’Arezzo, en passant par la Missa Hercules Dux Ferrarie de Josquin des Prez et le fameux motif BACH du dernier contrepoint de l’Art de la fugue comme la forme la plus ancienne de mapping, faisant correspondre des lettres à des hauteurs.

Les étapes préparatoires

Les deux étapes préparatoires les plus utilisées avant un processus de mapping sont sans doute :

le modulo
la normalisation

Le modulo est approprié pour traiter une séquence de données qui n’a pas de limite, comme une suite de nombres entiers. L’opération consiste basiquement à définir un seuil au-delà duquel la série numérique reprendra à partir du premier élément.

On peut présenter le modulo comme le reste d’une division entière (ou division euclidienne). Par exemple :

7 ÷ 2 = 3 reste 1. Ainsi, 7 modulo 2 = 1.

27 ÷ 24 = 1 reste 3. Ainsi, 27 modulo 24 = 3.

On utilisera le modulo 12 pour une musique dodécaphonique, le modulo 7 pour une musique diatonique, 88 pour l’ensemble des touches d’un clavier, 127 pour avoir l’ensemble des degrés d’une échelle MIDI, etc.
Lorsque, au contraire, les données de départ sont dans un étroit intervalle, alors il vaut mieux utiliser la normalisation.

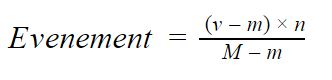
Où :

v : valeur à mapper
m : valeur minimale du jeu de données à mapper
n : nombre d’éléments dans le jeu de données à mapper
M : valeur maximale du jeu de données

Le tout exprimé en valeurs entières, sans prendre en compte d’éventuelles décimales.

Le résultat mappe les données dans un intervalle entre 0. et 1.

On peut éventuellement prévoir un mapping logarithmique, en mettant les valeurs à l’échelle à l’intérieur d’une courbe exponentielle inversée, par exemple sur des données fréquentielles, pour s’adapter aux “anamorphoses de la perception”.

Mapping déterministe vs mapping paramétrique

On appelle mapping déterministe celui qui fait correspondre, par exemple à chaque symbole d’un alphabet dans un L-système, la même valeur musicale à chaque fois (hauteur, intervalle, durée…). On parle de mapping paramétrique lorsque chaque donnée fournie par l’algorithme donne lieu à des consignes relatives à l’événement musical qui précède, donnant ainsi lieu à des résultats sonores différents selon le contexte.

Sonification et data bending

La sonification désigne au sens large la technique permettant de rendre sonore un ensemble de données. Mais, dans son sens le plus strict, il s’agit d’un outil scientifique destiné à représenter des données, afin d’aider à percevoir des variations pertinentes lorsque la visualisation ne le permet pas. A l’opposé, les techniques appelées “data bending” (littéralement : torsion de données) visent à produire des résultats sonores à partir de données sans chercher à ce que ces dernières restent lisibles. Le processus passe généralement par de la manipulation de fichiers informatiques d’un format donné dans un logiciel destiné à d’autres formats, pour un résultat généralement imprévisible, avec une grande proportion de bruit et “sale”.

Par exemple, on peut ouvrir un fichier (de préférence non compressé : .png, .exe…) dans un éditeur de son comme Audacity (en sélectionnant raw format, big-endian, U-Law, 44.1 kHz or larger quality). D’une certaine manière, on peut considérer que les prémices de ces techniques sont à chercher du côté des technologiques comme l’UPIC ou de synthétiseurs alternatifs comme l’ANS, qui convertissaient des données visuelles en données sonores.

La sonification en composition algorithmique prend place entre ces deux pôles, pouvant viser à transmettre de manière linéaire et aussi transparente que possible les données fournies par l’algorithme (en particulier si ce dernier a été soigneusement élaboré en vue de créer un matériau sonore précis) ou au contraire pouvant mettre l’accent sur les techniques de mapping.

Chaque donnée produite par les différentes techniques présentées ici se présente avec sa structure propre, parfois son format. Il y a des types de donnée qui invitent directement à certaines stratégies de mapping (comme la mélodie pentatonique générée par le dé à 6 faces), et des stratégies de mapping si sophistiquées que les données traitées y deviennent méconnaissables et indifférentes. Il appartient au musicien de trouver le point d’équilibre où l’utilisation d’un algorithme spécifique fait sens en fonction de son traitement sonore.

Comme l’écrit Paul D. Reiners, “un autre danger en utilisant des techniques complexes de mapping, c’est que l’on a tendance à y coder ses propres préjugés musicaux (qu’il soit occidentaux ou orientaux, tonal ou atonal). Ecrire un programme informatique capable de composer dans le style de Chopin ou de Bach presque aussi bien que Chopin ou Bach est certes un remarquable accomplissement, mais pourquoi nous limiter à cela ? Je pense que la composition algorithmique n’aura pas pleinement démontré son succès tant qu’elle ne sera pas capable, non seulement de créer de la belle musique, mais de créer de la belle musique d’un genre entièrement différent de ce que nous avons déjà pu entendre. […] Je pense que les meilleurs résultats viendront de l’usage des mappings les plus simples.” (traduction personnelle).

Pistes de lecture

(Illustration : Athanasius Kircher, Musurgia Universalis, Domaine public)