Fonctionnement

On désigne par l’expression “machine learning” les algorithmes qui apprennent en étudiant des exemples. L’objectif de cette technique est de faire des extrapolations, des généralisations à partir d’un ensemble de données (par exemple, apprendre à un algorithme à reconnaître un objet dans une image d’après un grand nombre d’images).

Un neurone artificiel est une fonction mathématique mettant en relation des entrées x avec des sorties y, mimant le modèle physiologique de la transmission d’un signal électrique dans les véritables neurones d’un cerveau.

Pour activer un neurone, on considère la somme des signaux reçus en entrée de ce neurone en appliquant un coefficient à chacun (le poids, ici représenté par la lettre p). On parle de somme pondérée. Au-delà d’un certain seuil (= seuil d’activation, ici représenté par la lettre s), le neurone s’active et produit un 1. Le mécanisme d’activation du neurone artificiel peut se représenter schématiquement de la manière suivante :

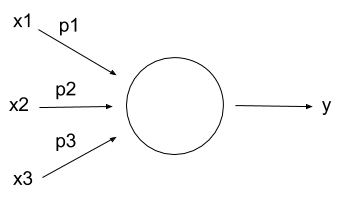
p1x1 + p2x2 + p3x3    > s ? → y = 1

< s ? → y = 1

La phase d’apprentissage est le processus permettant au réseau d’associer un stimulus donné à une réponse, et consiste à faire varier les valeurs (p et s) jusqu’à ce que le lien se fasse correctement entre deux ensembles de données.

On peut distinguer grossièrement deux principales méthodes d’apprentissage :

• apprentissage supervisé, consistant à montrer au réseau de neurones des exemples de couples de vecteurs entrée/sortie afin qu’il mémorise les associations.
• apprentissage non supervisé (ex : les SOM), où l’on n’a pas recours à des exemples pendant la phase d’apprentissage. A chaque entrée, c’est le neurone dont le vecteur des poids synaptiques ressemble le plus au vecteur d’entrée qui est est activé, et son poids synaptique modifié pour ressembler encore plus au vecteur d’entrée. Il a donc plus de chances d’être choisi lors de la présentation de l’entrée suivante.

L’apprentissage est l’un des traits caractéristiques des neurones artificiels, qui peuvent ainsi “résoudre” un problème donné sans que ce dernier ne soit entièrement formalisé. Il s’agit de présenter à l’algorithme des exemples pertinents et en nombre suffisant, et de choisir l’architecture de neurones la plus adaptée à la situation.

On parle ensuite de phase de prédiction (la phase générative à proprement parler) lorsque l’algorithme, une fois entraîné, est capable d’extrapoler une valeur y à partir d’une valeur x.

C’est ce fonctionnement linéaire à seuil qui permet de “généraliser”, puisque le réseau associe nécessairement une réponse à l’une ou l’autre des valeurs (0 ou 1).

Un réseau consiste à associer plusieurs neurones de manière à multiplier la capacité de la machine à traiter un problème complexe. Il existe un très grand nombre de configurations de réseaux possibles. Mais on peut en distinguer deux principales :

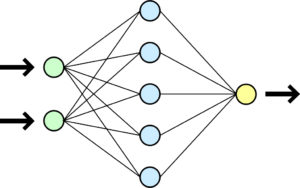
• réseaux à couches (le signal va de la gauche à la droite, chaque neurone d’une couche communique avec tous les neurones de la couche suivante)

• cartes topologiques, ou cartes auto-organisatrices (ou SOM, pour Self Organizing Map, ou encore cartes de Kohonen). Ce modèle s’inspire des recherches en neurophysiologie, qui ont mis en évidence que certaines informations étaient traitées dans certaines zones spécifiques du cerveau. Ces réseaux sont structurés en zones regroupant les neurones sensibles aux mêmes catégories de vecteurs.

Les cartes topologiques peuvent être de plusieurs types, par exemple :

• ROSOM : carte auto-organisatrice récurrente oscillatoire
• PMC : Perceptron Multi-couche

En musique

Dès les premières expériences de composition assistée par ordinateur (ILLIAC Suite), une question se pose : face à l’impossibilité de modéliser l’intégralité des règles (en grande partie instinctives et comportant de nombreuses exceptions) qui régissent une composition musicale, sur quels critères se baser pour faire un choix ? C’est l’une des situations où les réseaux de neurones, par leur capacité à imiter le fonctionnement du cerveau humain pour identifier des règles déterminantes, peut jouer un rôle intéressant. La technologie des réseaux de neurones s’illustre dans des domaines très variés, allant de la détection de hauteurs, la reconnaissance de timbre, à l’analyse de style musical, voire la compréhension de la perception musicale, comme dans le système imaginé par Jamshed J. Bharucha et Katherine Olney (“La cognition tonale, l’intelligence artificielle et les réseaux neuronaux”, dans La musique et les sciences cognitives) pour simuler la manière dont une oreille occidentale comprend la musique traditionnelle indienne, en entraînant un réseau à reconnaître une tonalité majeure ou mineure, puis en présentant à ce réseau des râgas indiens, obligeant ainsi l’automate à attribuer une tonalité occidentale à chaque râga.

Dans le domaine de la création musicale proprement dite, bien souvent, les musiciens s’intéressent davantage au processus mis en oeuvre par les réseaux neuronaux qu’au résultat. L’artiste Frédéric Voisin utilise ainsi les cartes auto-organisatrices en privilégiant la phase d’apprentissage, jusqu’à délibérément réduire l’efficacité du système et “diminuer [leur] vitesse d’apprentissage […], étant donné que l’efficacité de l’algorithme à la base de ces réseaux les amenait à optimiser leurs performances trop vite”.

La dimension interactive est également une caractéristique structurelle des réseaux neuronaux. Mathieu Sauneuf (Réseaux de neurones artificiels et composition musicale électroacoustique) écrit que même “lorsque les spectateurs ne sont pas invités à interagir avec le système, l’installation doit faire démonstration de la situation d’interactivité existant entre les agents neuromimétiques et leur environnement. Dans le cas contraire, la virtuosité poïétique à l’origine de l’installation ne trouve pas son écho dans l’esthétique de l’oeuvre.”

Jocelyne Kiss : Expérience d’après Klavierstück IX de Stockhausen

Dans “Composition musicale et sciences cognitives, Tendances et perspectives”, Jocelyne Kiss décrit de manière détaillée une expérience de modélisation par neurones artificiels d’après le Klavierstück 9 de Karlheinz Stockhausen.

Le principe est le suivant : un générateur aléatoire présente au réseau de neurones différents remplissages rythmiques d’une mesure à 3/8 (l’une des mesures les plus utilisées dans la composition originale de Stockhausen), et ce dernier doit identifier, en fonction de son apprentissage, quelles sont les cellules qui appartiennent au style du compositeur allemand.

Les données rythmiques sont codées sous forme de bits (les 3 premiers sur le type de division, les suivants sur les figures rythmiques).

Jocelyne Kiss insiste sur l’importance de choisir la bonne architecture pour le réseau de neurones, mais aussi un système suffisamment souple pour pouvoir le reprogrammer facilement en cas de phase d’apprentissage infructueux. En effet, “un nombre trop faible de cellules attribuera au réseau des ressources insuffisantes pour effectuer la séparation des formes envisagées ; à l’inverse, un nombre trop élevé de cellules cachées engendrera un excès de précision dans la séparation des formes et le réseau pourra retenir à partir de l’ensemble d’apprentissage des aspects insignifiants de quelques exemples”. Afin de trouver l’équilibre optimal, elle se rapporte à un principe empirique stipulant que le nombre de neurones dans le réseau doit suivre une forme pyramidale, en décroissant de la couche d’entrée vers la sortie (dans un réseau à 3 couches, avec n neurones d’entrée et m de sortie, avec n > m, il y aura  neurones cachés). Elle choisit donc un réseau à 3 couches avec :

• 19 cellules d’entrée (la totalité des types de mesures rythmiques envisagés dans cette expérience pouvant être codées sur 19 bits)
• 5 cellules cachées
• 1 cellule de sortie (une seule réponse est proposée : la cellule présentée s’apparente au style de Stockhausen, oui ou non)

Robin Meier : For Alan Turing

For Alan Turing (2004) de Robin Meier est une oeuvre pour piano et électronique en temps réel. Pour donner à entendre le processus d’imitation du réseau de neurones, le musicien imagine un dispositif scénique où le fonctionnement du neurone est en quelque sorte latéralisé : un piano virtuel diffusé par les haut-parleurs à la gauche de la scène imite un autre piano virtuel situé à droite, pendant que “l’interprète” influe sur le comportement de l’algorithme en modifiant en temps réel le taux d’apprentissage du premier neurone et ainsi la ressemblance ou la dissemblance des deux instruments virtuels.

Le module se compose d’un neurone (sur le principe d’un SOM), dont la sortie est envoyée à un autre SOM de 25 neurones, chargé d’imiter la sortie du premier. Les valeurs prises en compte, en format MIDI, sont la hauteur, la vélocité et la durée des notes.

Pistes de lecture

• Mathieu Sauneuf, Réseaux de neurones artificiels et création musicale électroacoustique
• Robin Meier, Modèles de la cognition et leurs expérimentations artistiques
• Joey Rogers, Object-oriented Neural Networks in C++

 

(Illustration : Nicolas P. Rougier, Neuron-SEM-2, Licence GNU GPL)