INDEX
1 – Origine
2 – Principe de base
3 – Représentations graphiques
4 – Différents types de L-Systèmes
5 – Stratégies de sonification
6 – Oeuvres à base de L-Systèmes
7 – Pistes de lecture
Origine
Inventé par le botaniste néerlandais Aristid Lindenmayer, les systèmes de Lindenmayer (que nous appellerons pour plus de facilité L-système, par analogie avec l’usage anglo-saxon) permet de décrire le développement des arbres, champignons, algues et levures. Il fut développé avec l’aide de l’informaticien canadien Przemysław Prusinkiewicz, ce dont témoigne leur livre commun “The Algorithmic Beauty of Plants”. Les L-systèmes sont souvent reconnus comme parmi les plus simples et les plus puissants algorithmes capables de décrire les mécanismes de croissance observés dans la nature.
Principe de base
Il s’agit d’un algorithme récursif, ou grammaire formelle. On définit une règle syntaxique permettant de transformer un symbole en une chaîne de symboles.
Par ex :
P1: b est remplacé par aba quand il est placé avant un a
P2: b est remplacé par bab quand il est placé après un a
P3: b est remplacé par baa, quand il est placé entre deux a
Représentations graphiques
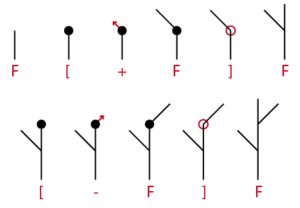
Une des représentations graphiques les plus communes des L-systèmes est la tortue de Seymour Papert (ou courbes de Peano). Les commandes utilisées sont habituellement :
F Avance d’un pas de longueur d en traçant une ligne
f Avance d’un pas de longueur d sans tracer de ligne
+ Tourne à gauche d’un angle a
– Tourne à droite d’un angle a
Pour décrire l’état à un moment t de la tortue, on a donc besoin d’un triplet (x, y, a) décrivant ses coordonnées x et y et décrivant sa direction actuelle a.
Ce système permet de dessiner uniquement une courbe. Pour obtenir une autre représentation connue, l’arborescence, on doit étendre le “vocabulaire” avec des symboles permettant de rester en position (traditionnellement : [) et de revenir en position arrière (traditionnellement : ]).
Exemple :
δ = 45°
d = 2
F[+F]F[-F]F
Ajouter de la complexité
On peut ajouter des symboles sans traductions graphiques pour simplement ajouter de la complexité au système.
Exemple (source : Philip Galanter) :
ω : X
p1 : X → F[+X]F[-X]+X
p2 : F → FF
n = 0; X
n = 1; F[+X]F[-X]+X
n = 2; FF[+F[+X]F[-X]+X]FF[-F[+X]F[-X]+X]+F[+X]F[-X]+X
Différents types de L-systèmes
Il existe plusieurs grandes catégories de l-systèmes, parmi lesquelles :
- L-systèmes stochastiques
- L-systèmes contextuels
- L-systèmes paramétrique
L-systems stochastiques
Chaque expression peut donner lieu à plusieurs états possibles, avec des probabilités différentes. Exemple inspiré de Stelios Manousakis :
Alphabet :
V : A B
Règles de production :
P1 : A =70%→ AB
P2 : A =30%→ BA
P3 : B => A
Axiome :
ω : A
Ce qui peut produire par exemple :
n0 : A
n1 : AB
n2 : ABA<
n3 : BAAB
n4 : ABAABBAA
Ou bien (parmi d’autres possibles) :
n0 : A
n1 : BA
n2 : AAB
n3 : ABABA
n4 : BAABAAAB
L-systèmes contextuels
Nous avons vu jusque là des systèmes “Context-free”, dans lesquels la règle est appliquée pendant tout le processus. Dans les L-systèmes contextuels, un peu comme dans les chaînes de Markov de 2ème ordre, le résultat dépend de la dernière situation. Ce mécanisme permet de diffuser un “signal” le long de la structure en forme de branche, qui va déterminer l’emplacement de certaines branches (par exemple), permettant de simuler les hormones ou les déclencheurs chimiques.
ω : baaaaaaaa
p1 : b < a → b
p2 : b → a
Si a est après b, il devient b
b devient a
baaaaaaaa
abaaaaaaa
aabaaaaaa
aaabaaaaa
aaaabaaaa
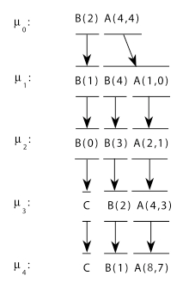
L-système paramétrique
Les règles d’un L-système paramétrique se présentent comme suit :
F(x) F(x constante)
Exemple :
ω : B(2) A(4, 4)
p1 : A(x, y) : y ≤ 3 → A(x × 2, x + y)
p2 : A(x, y) : y > 3 → B(x) A(x/y, 0)
p3 : B(x) : x < 1 → C
p4 : B(x) : x ≥ 1 → B(x – 1)
Stratégies de sonification
Il semblerait que les indiens Shipibos au Pérou, dont les broderies ont des motifs fractals qui rappellent fortement les L-Systèmes, seraient en mesure d’interpréter ces motifs vocalement, et réciproquement chantent toujours lorsqu’ils créent les motifs. Mason et Saffle prétendent que toute ligne mélodique peut-être modélisée par un L-Système, ce qui suggère des possibilités d’extrapolation de mélodies pré-existantes. Ils mettent également en évidence la dimension fractale propre à toute mélodie dans les cultures occidentales et non-occidentales, en se basant sur les travaux de Narmour et de Charles R. Adams.
Le compositeur Nigel Morgan utilise ce système dans plusieurs de ses pièces, notamment Treeness pour violon et orgue positif.
Il existe des méthodes très différentes de sonification, certaines basées directement sur le résultat de l’algorithme, d’autres passant au préalable par une représentation graphique. L’un des avantages de cet outil est qu’il peut être utilisé aisément sans l’aide d’un ordinateur.
Méthode Tom Johnson
Tom Johnson, dans l’un des mouvements de sa pièce Automatic Music pour 6 percussionnistes, utilise un L-système directement sonifié avec un alphabet simple (chaque percussionniste dispose d’une note aiguë et d’une note grave, 1=note grave; 2=note aiguë, 3=silence).
ω : 1
Et règles :
p1 : 1 → 1 1 2
p2 : 2 → 3 2
p3 : 3 → 3 3
Cela donne :
112
11211232
1121123233321121123211211232333233333332
…
Méthode Prusinkiewitz
Cette technique, proposée par l’un des créateurs des L-systèmes, passe par la représentation graphique en tortue avant de traduire l’algorithme en paramètres mélodiques.
Il s’agit d’interpréter les lignes horizontales comme des durées et les lignes verticales comme des intervalles :
- Si la courbe commence par une ligne horizontale, on choisit par convention la première note de l’échelle choisie (dans l’exemple => do).
- Si la courbe commence par une ligne verticale, on choisit par convention la note obtenue en appliquant l’intervalle de cette première ligne à la première note de l’échelle choisir (par ex : ligne verticale descendant de 2 pas => la).
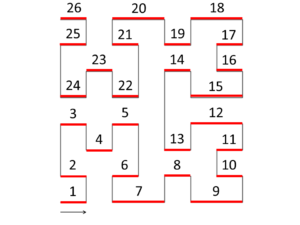
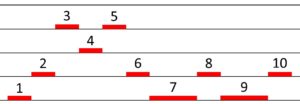
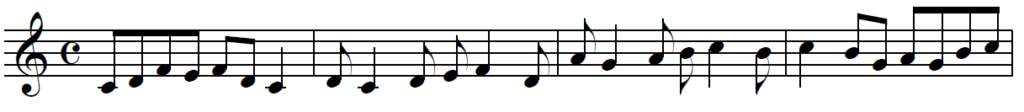
On peut lire une courbe par les deux bouts, et lui faire opérer des rotations, ce qui permet de générer jusqu’à 8 versions mélodiques d’une même courbe (sauf cas de palindrome) :
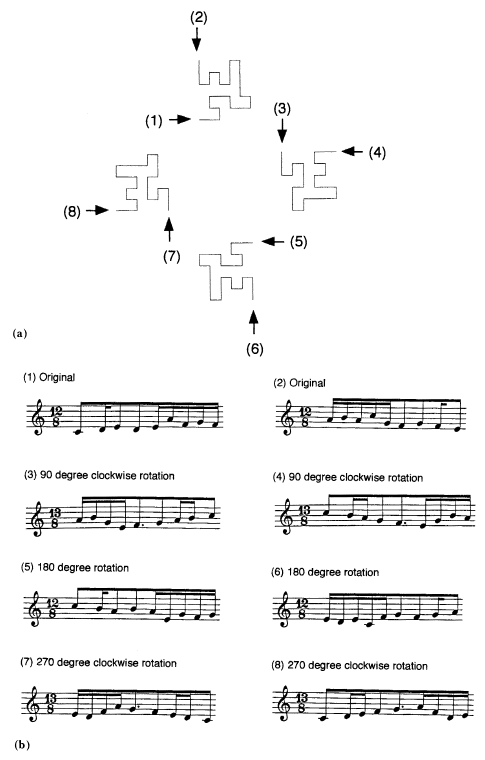
On peut créer des contrepoints en lisant simultanément les mélodies issues de deux rotations d’une même courbe (ce que l’on pourrait considérer comme un équivalent visuel du canon musical).
Prusinkiewitz a également proposé une utilisation des mélodies en l-systèmes pour générer de la musique indienne carnatique.
Méthodes Roger Luke DuBois
Dans sa dissertation “Applications of Generative String-Substitution systems in Computer Music”, Roger Luke DuBois propose plusieurs méthodes de mapping de L-systèmes.
L’une d’elle permet de générer des séquences mélodiques à partir d’un vocabulaire réduit à 2 signes.
Le système (sensible au contexte) fonctionne avec les règles suivantes :
ω : BAB
p1 : A<B>B → BA (si B est placé entre A et B, il devient BA)
p2 : A<A>B → AB (si A est placé entre A et B, il devient AB)
p3 : A<A>A → B (si A est placé entre A et A, il devient B)
p4 : B<A>* → AA (que A soit placé entre B ou A, il devient AA)
n0 : BAB
n1 : BAAB
n2 : BAAABB
n3 : BAABABBAB
n4 : BAAABBAABABAAB
n5 : BAABABBABAAABBAABAAABB
Le mapping se fait ensuite en deux étapes. D’abord, on génère les hauteurs, en considérant le B comme une note et le A comme un intervalle, selon que :
Ø = 1 demi-ton
A = 2 demi-tons
AA = 3 demis-tons
etc.

(Samples : Sonatina Symphonic Orchestra, Creative Commons CC-BY)
Puis on applique la règle suivante pour les durées :
B = double croche (attaque)
A = double croche (liée à la note précédente)

Autre proposition, à partir de cet autre système sensible au contexte :

qui s’apparente à un automate cellulaire à 1 dimension fonctionnant avec la règle suivante :

Il génère ce qu’on appelle un triangle de Sierpinski (ici les 100 premières itérations) :
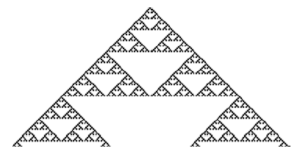
En considérant que B représente une hauteur, on mappe les 80 cellules à un espace sonore allant de G#0 à E7 pour les 128 premières générations :

Il propose également des méthodes de mapping paramétrique. Il s’agit alors de considérer les symboles comme des instructions successives (comme dans la visualisation de la tortue) affectant la situation créée par les symboles précédents.
Par exemple :
F Joue une note à la dernière hauteur jouée de la dernière durée jouée
G Joue une note une tierce mineure plus haute que la dernière note, de la dernière durée jouée
– Transpose la dernière hauteur à la quinte inférieure
+ Transpose la dernière hauteur à la quinte supérieure
Q Réduire la durée de 125 ms
Y Augmente la durée de 125 ms
De façon conventionnelle, on définit la note de départ comme le do central à 500ms.
Chaque symbole = 125 ms. Pour tout symbole autre que F et G, cela prolonge la note précédente, créant ainsi un rythme. Ainsi, les générations 1 à 5 de :
n0: F
n1: +GQ
n2: +FY-F-FG+
n3: ++GQ+GF–+GQ-+GQFY-F+
n4: ++FY-F-FG++FY-F+GQ–+FY-F-FG+-+FY-F-FG++GQ+GF–+GQ+
n5: +++GQ+GF–+GQ-+GQFY-F+++GQ+GF–+GQ+FY-F-FG+–++GQ+GF–+GQ-+GQFY-F+-
++GQ+GF–+GQ-+GQFY-F++FY-F-FG++FY-F+GQ–+FY-F-FG++
Donnent :

Comme pour toute technique de mapping paramétrique, la perception du L-système risque cependant d’être beaucoup plus difficile qu’avec un mapping où chaque symbole a toujours la même traduction sonore.
Oeuvres à base de L-systèmes
- Nigel Morgan, Treeness
- Maxwell Tfirn, 32o(F+F)F[+F][-F]F[-F[-F][+F]F]
Pour expérimenter
- Michael Norris : L-System Generator
- Tim Thomson : Tune Toys – Expresso
(Illustration : Biodiversity Heritage Library, CC-BY-NC-SA)
