Issu originellement des arts décoratifs et de l’architecture, le concept de pavage désigne la partition d’un espace donné par un motif répété. Il s’agit ici de présenter des techniques basées sur des répartitions hautement organisées des événements sur une durée, soit pour neutraliser tous les rapports métriques en brisant toute répétition, comme dans le cas de la règle de Golomb, soit pour atteindre une uniformité maximale comme dans les rythmes euclidiens.
Il est intéressant de noter que la recherche paradoxale d’une forme d’uniformité musicale (par la saturation de l’espace sonore, par le développement de variations aux limites de la perception…) fait partie des idées importantes qui ont traversé l’histoire de la musique du XXe siècle, par des figures telles que György Ligeti, Morton Feldman, ou encore Zygmunt Krauze dans sa période “uniste”.
INDEX
1 – Canons rythmiques, canons de Vuza
2 – Règle de Golomb, “rythmes plats” et accords tous-intervalles
3 – Rythmes euclidiens (ou algorithme de Bjorklund)
4 – Pistes de lecture
Canons rythmiques, canons de Vuza
Le canon rythmique, appellation abrégée de ce qu’on nomme plus précisément “canon rythmique mosaïque” (tiling canon, en anglais), est un canon portant uniquement sur la dimension rythmique, ayant comme contrainte qu’une seule voix soit entendue sur chaque temps, et que, mises en boucle, l’ensemble des voix “pavent” de façon continue la grille temporelle sans laisser de silence.
![]()
![]()

Dans la littérature scientifique, les canons rythmiques sont volontiers notés de façon numérique, sous forme de deux listes entre crochets représentant successivement le rythme interne et le rythme d’entrée des voix. Dans le cas de notre exemple :
[101000000110010001000000][100000100000100000100000]
Ou bien, sous forme de durées :
[2,7,1,3,4,7] [6,6,6,6]
![]()

(Samples : CASA DA MÚSICA’s VIRTUAL GAMELAN, CC-BY)
Dans un canon rythmique, le schéma métrique du motif lui-même (rythme interne) et le schéma rythmique des entrées des voix (rythme externe, ou rythme “dual”, ou “outer rhythm” en anglais) sont interchangeables : un canon rythmique en résulte dans les deux cas. Autrement dit :
- le nombre de voix du premier canon devient le nombre d’impacts (ou de notes, ou d’attaques) du second (et réciproquement, le nombre d’impacts du premier devient le nombre de voix du second)
- le rythme des entrées des voix du premier devient le rythme interne du second
![]() =>
=>
![]()
- et le rythme interne du premier devient le rythme d’entrée des voix du second
![]() =>
=>

Voici ainsi le canon « dual » qui résulte du canon précédent :
![]()
![]()
On constate sans peine que la périodicité rend cependant le résultat musical beaucoup plus pauvre. C’est là qu’intervient la particularité des canons de Vuza.
Les canons de Vuza, du nom du professeur de mathématique roumain Dan Tudor Vuza qui les étudia pendant dix ans, sont une sorte particulière de canon rythmique sans périodicité interne, c’est-à-dire que ni le rythme du motif ni le rythme “dual” ne se reproduisent à l’intérieur de la durée totale du rythme. Ils sont très rares (de l’ordre de un sur plusieurs millions de canons rythmiques possibles) et la plus “petite” périodicité est 72 (puis 108, 120, 144…), avec au moins 6 voix.
Exemple du canon de Vuza de durée 72 à 6 voix [19,1,4,1,6,13,4,7,6,6,1,4] [38,8,8,2,8,8] :
![]()
Et son dual (donc à 12 voix) :
![]()
Il est possible d’expérimenter les canons rythmiques par des listes pré-existantes, telles que celles-ci :
- Liste des canons rythmiques de longueurs comprises entre 2 et 40
- Liste complète des canons de Vuza à 72 temps
- Liste complète des canons de Vuza à 108 temps
Il existe également des objets Open Music permettant de trouver des canons rythmiques.
Esthétiquement, les canons de Vuza offrent ce que Messiaen appellerait sans doute “le charme des impossibilités”, étant sans doute la forme la plus désordonnée (pour la perception) en même que temps que la plus hautement organisée. Certains compositeurs ont d’ailleurs exploité cet aspect déstabilisant de régularité sans repère répétitif, comme George Bloch dans son « Projet Hitchcock », autour du film Vertigo. L’une des particularités de ces canons est qu’ils ne sont a priori pas perçus comme des structures contrapuntiques, mais plutôt comme des moto perpetuos ou des textures.
En musique, ils sont explorés par les compositeurs depuis la fin des années 1990. Quelques exemples de pièces qui utilisent les canons de Vuza :
- Sébastien Roux, Cinq canons de Vuza (2015)
- Tom Johnson, Tilework (2003)
- Fabien Levy, Coïncidences (1999)
- Mauro Lanza, La Descrizione del Diluvio (2008)

Règle de Golomb, “rythmes plats” et accords tous-intervalles
De nombreux chercheurs ont recherché les lois à l’origine des proportions harmonieuses des chefs-d’oeuvre de l’histoire de la musique, dans le principes des fractales, le bruit 1/f, etc. Que se passerait-il si l’on se posait la question inverse, et que l’on se demandait quelle organisation des sons répondrait le moins à une perception de cohérence et d’équilibre ? C’est ce qu’a fait Scott Rickard, en imaginant le principe qui donnerait naissance à la “musique la plus laide du monde”, à l’aide de la règle de Golomb.
Une règle de Golomb est une règle munie de marques disposées à des rapports entiers, de sorte qu’il n’y ait pas deux marques à la même distance l’une de l’autre.
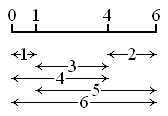
En musique, l’utilisation de cet algorithme conduit donc à une éradication totale de la répétition, bien plus forte qu’avec de l’aléatoire.
- L’ordre d’une règle de Golomb est le nombre de marques qu’elle porte (graduation 0 comprise). Notre exemple est une règle d’ordre 4.
- La longueur d’une règle de Golomb est la plus grande distance entre deux de ses marques. Dans notre exemple, la longueur est de 6.
- On nomme règle de Golomb optimale la plus courte règle de Golomb pour un ordre donné. Notre exemple est bien une règle optimale. La règle de Golomb [0,1,3,7] est une règle d’ordre 4 non optimale.
- On nomme règle de Golomb parfaite la règle contenant toute les distances possibles à l’intérieur de la règle. L’exemple est une règle parfaite à 4 marques.
Jusqu’à présent, des règles de Golomb jusqu’à 26 graduations seulement ont pu être construites.
En connectant le début de la règle de Golomb à la fin et en considérant chaque marque comme un impact, on obtient un rythme. Selon la terminologie de Jon Wild, on peut parler de « rythme plat » car l’histogramme des rapports entre les différentes durées est toujours compris entre 0 et 1.
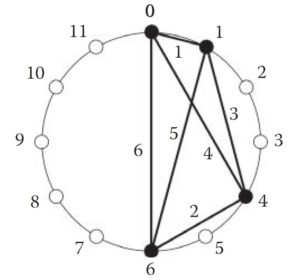
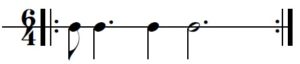
Appliquées au domaine des hauteurs, deux des règles de Golomb d’ordre 4 correspondent à ce qu’on appelle les “tétracordes tous intervalles” (All-Interval tetrachord), bien connus en musique, et notamment utilisés par Elliott Carter, pour leur capacité à garantir un matériau réduit mais favorisant le maximum de diversité mélodique et harmonique.
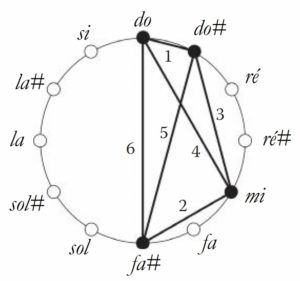

Il est très facile de créer des rythmes plats à 3 marques, car il suffit de dessiner un triangle où aucun des trois côtés n’est de même longueur (donc pas de triangle isocèle). La difficulté pour créer des rythmes plats commence quand on dépasse les 3 impacts. Exemples à 4 impacts :
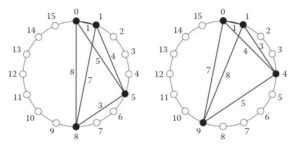
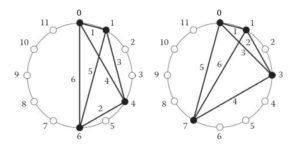
Rythmes euclidiens (ou algorithme de Bjorklund)
L’algorithme de Bjorklund répond au problème suivant : comment répartir de façon uniforme un certain nombre d’impacts rythmiques dans un nombre d’unités rythmiques dont il n’est pas le multiple ? Par exemple, comment répartir de façon aussi uniforme que possible 5 pulsations dans 13 unités de mesures ?
Pour cela, le physicien E. Bjorklund a inventé un algorithme exploitant le principe des divisions euclidiennes : il s’agit à chaque étape de chercher à construire des séquences de plus en plus longues.
Prenons par exemple le rythme euclidien où 5 pulsations doivent être réparties sur 13 temps :
[1 1 1 1 1 0 0 0 0 0 0 0 0]
On associe d’abord un zéro pour chaque un, produisant ainsi 5 séquences de 2 bits et 3 zéros restants :
[10] [10] [10] [10] [10] 0 0 0
On distribue ensuite les zéros restants de la même façon :
[100] [100] [100] [10] [10]
On peut encore prolonger l’opération et créer des séquences plus longues :
[10010] [10010] [100]
Le processus s’interrompt lorsqu’il n’est plus possible de construire des séquences identiques plus longues :
[1 0 0 1 0 1 0 0 1 0 1 0 0]
Le fonctionnement de l’algorithme de Bjorklund suit la même logique que l’algorithme d’Euclide par le regroupement des éléments et la réutilisation des restes, de manière itérative.
Godfried Toussaint a démontré qu’un grand nombre des rythmes obtenus par cet algorithme étaient des rythmes utilisés dans les musiques traditionnelles du monde entier, en particulier ceux sur un nombre d’unités de mesure entre 3 et 24 (les plus longues séquences étant utilisées dans les musiques traditionnelles centrafricaines).
Rhythm Necklaces from meara o’reilly on Vimeo.
Il définit également plusieurs catégories de rythmes euclidiens : les chaînes euclidiennes, les chaînes euclidiennes inversées, et les rythmes euclidiens qui ne sont pas des chaînes (rythmes restant inchangés lorsqu’on leur fait subir un miroir sur l’axe central dans une représentation circulaire).
Pistes de lecture
- Emmanuel Amiot, Canons rythmiques.
- Tutoriels pour construire des canons rythmiques mosaïques dans OpenMusic
- Patch Pure Data utilisant les rythmes euclidiens.
- Godfried Toussaint, « The Euclidean Algorithm Generates Traditional Musical Rhythms« , Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science, Banff, 2005.
- Tom Johnson, Tiling the Line in Theory and in Practice.
(Illustration : Caetano Candal, Parede, CC-BY)
